The dialog below asks for the size of the LP model to be used in the exercise and the selects the Solution Option to be Instruction. The latter controls how intermediate information is presented to the student.

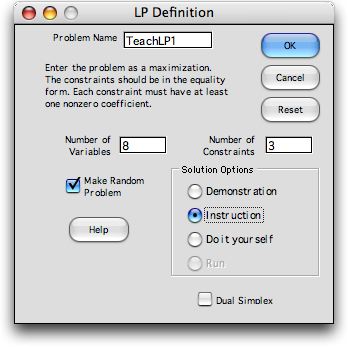
As noted on the dialog, the problem is to be entered in the equality form, so the number of variables should include the slack or surplus variables necessary to convert inequalities into equalities. All variables are assumed to be nonnegative. The maximum dimensions for this program is 20 variables and 10 constraints.

When the checkbox labeled Make Random Problem is checked, random numbers are used to generate data for the model. Otherwise, the model coefficients are entered as 0.

Three solution options are available. The Demonstration option goes through each iteration of the primal simplex with simple explanations about how the simplex technique operates. The student only clicks progress buttons to move the demonstration along. The Instruction option allows the student to choose the variables that are to enter and leave the basis. Hints are provided at various points to aid the student in the process. The Do it yourself option leaves the decisions entirely up to the student. The program performs pivot operations initiated by the student.

The randomly generated model used as an illustration in this section is shown below.

The random model has all nonnegative integer coefficients. The constraints are less than or equal to constraints, and the last three variables are slack variables.

The coefficients in the model can be changed in any way. For the example, we have modified the coefficients in column 6. Since an initial basis is not readily apparent for the revised problem, the modification requires the use of an artificial variable.

When the model is ready, press the Start button. Because an initial basis is not available, the program asks whether an artificial variable should be added.

With a positive response, the program provides an artificial variable, art1, to construct the initial basis. A two phase method is used. In Phase 1, the vector C1 provides the objective coefficients. Only the artificial variables have nonzero cost coefficients (-1). Since the algorithm is maximizing, the artificial variables will be made as small as possible during Phase 1. If they go to zero, the solution obtained is feasible for the original LP model. If Phase 1 does not drive the artificial variables to zero, no feasible solution exists and the algorithm terminates. To begin the iterative portion of Phase 1, press on the Phase 1 button on the worksheet.

The tableau is constructed by the program with the initial basis provided by either slack or artificial variables.

The tableau is located below the LP model on the worksheet as in the figure above. As the algorithm progresses, the view of the worksheet is focused on the tableau. Cells indicate the Phase and Iteration number. The cells near the center of the display show the variables that enter and leave the basis. In this initial state, the values shown have no meaning. The portions of the worksheet colored yellow are controlled by the program and generally should not be changed by the student. One exception is the column of red numbers labeled Basic Index. Although generally, the computer will control these numbers, for some exercises the student may wish to manipulate the numbers directly.

Pressing the Iterate button begins the solution process. For the primal simplex algorithm, the first decision is to select some variable to enter the basis. In the Instructional Mode the dialog box asks for the index of the variable to enter the basis. Initially the index field is blank, but pressing the Hint button, causes the negative reduced costs in the tableau to be colored as shown. The index with the most negative reduced cost is inserted in the dialog box. The Hint button is not available in the Do it yourself mode.

Accepting the selection of the entering variable, the next dialog asks for the index of the variable to leave the basis. Again the Hint button colors the appropriate ratios and suggests the correct leaving variable. Note that the variable is specified by its index, not by the row it represents in the tableau.

After accepting the selection of the leaving variable, the pivot row and column are colored orange, and the pivot button is placed on the worksheet.

Pressing the Pivot button causes the program to adjust the tableau for the new basic variables as shown below.

For this example, the iteration has resulted in a zero value for the artificial variable. The solution is optimal for Phase 1. Pressing the Phase 2 button causes the original objective coefficients to be used for the computation of the reduced costs, row 0 of the tableau. The basic variables are the same for the tableau, but the new reduced costs are computed with the Phase 2 objective coefficients.

Pressing the Iterate button initiates the sequence of activities that leads to the next tableau.

One more iteration is necessary to find the optimal solution.

The final solution appears in the x-vector of the original LP model.