The capital budgeting model considers risk by computing the statistical variance (and standard deviation) of each project and selecting the projects to minimize the portfolio variance. To create a model that explicitly considers risk, click the Include Variance box on the dialog.

We use the previous example but assume that the initial investment, net income, and salvage value of each project are random variables with specified mean values and standard deviations. For this analysis the life of a project is not a random variable, but is fixed. Although it is sometimes convenient to assume Normal distributions for the random variables, it is not necessary for these results. The data for the projects in the example problem are shown in the table below. We assume that all random variables are statistically independent.

The mean values for the investment, net income and salvage are given for the example in rows 28 through 30 and the corresponding standard deviations are given in rows 36 through 38. The project lives are in row 31.

Using basic definitions for the mean and variance, it can be shown that the weighted sum of independent random variables is a random variable whose mean and variance are calculated as below.

Since the present worth values are computed as a weighted sum of the components, the mean and variance for the NPW for each project are computed as below. With the simple data option, these formulas are not used. Rather the NPW and standard deviation for each project are entered directly as data. The variance is the square of the standard deviation.

In the Excel table showing the example earlier on this page, row 32 holds the values of the mean NPW for each project, row 39 holds the values of the variance. Row 40 is the square root of row 39, and holds the standard deviations of the projects.

Using the same principles, the mean and variance of the portfolio can be expressed as functions of the decision variables. When the variables are constrained to 0 and 1, the variance is a linear function of the variables. Otherwise, the variance is a separable quadratic function of the variables.

With these definitions, several optimization models are possible depending on the goal of the analyst and the constraints that are included. We choose to minimize the variance while placing a lower bound constraint on the NPW. We also include a budget constraint. The figure below shows the model when the selection variables are limited to 0 or 1, representing not select or select. Since the model is linear, integer-linear programming can be used to find the optimum portfolio of projects.

The worksheet below shows the minimum variance solution for the example. Cells K20 and K21 are provided to hold the return goal (the minimum NPW) and the Budget respectively. These are controlled by the analyst. Of course when the cells are changed the model must be solved to obtain the new solution. The solution below has the smallest variance when the portfolio goal is to return at least 200. The budget constraint of 650 is not tight for this solution since the portfolio investment is only 400.

When variables are allowed to assume values greater than 1 or the integrality restriction is dropped, the optimization model is nonlinear. Larger values are allowed if more than one of each project can be purchased. One might drop integrality when the investments can be made in fractional amounts.

The Excel model for this case has additional rows for lower and upper limits on the variable values. The minimum variance solution is shown below when the return goal is 200. It happens to be the same as the binary case.

By sequentially solving this problem with different limits on the NPW constraint, the analyst can construct a set of solutions each with the minimum variance for the obtained value of the NPW. We illustrate with the model having binary variables. We set the budget for the example problem to be very large and not constraining and solve the problem for increasing limits on the NPW. A set of solutions is obtained. Plotting the solutions on a chart with NPW and variance as the axes, one obtains what is called the efficient frontier of solutions. 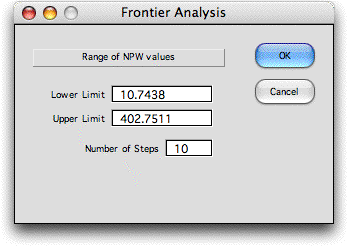To find the efficient frontier choose the Frontier action. The program finds the lower limit by setting the NPW constraint limit to 0 and solving the model. The lower limit obtained is the NPW of the minimum variance portfolio. The upper limit is the sum of the positive project NPW values. To make a more refined search, these limits may be changed. The Number of Steps entry specifies how many individual problems are solved. The NPW range is divided into this number of equal intervals.

The set of solutions for the example is shown below. The higher range of NPW values was not obtainable because of the budget constraint. Portfolios with higher returns have higher standard deviation values. Each portfolio shown is a minimum variance portfolio.

It is conceivable that projects are not statistically independent. The returns of dependent projects could be related through a correlation matrix. Minimizing the variance considering correlation becomes a non-separable quadratic programming problem. The binary version has the form of a quadratic assignment problem. Although the original program included this option, we have deleted it because of difficulty of solving the problem with the Excel Solver. Also, it seems unlikely that correlation data would be available in a practical instance of the capital budgeting problem.