The regression forecast is based on the assumption of a model consisting of a constant and a linear trend.

For the purposes of a forecast where the parameters of the model may change, it is more convenient to express the model as a function of , where is the positive displacement from a reference time T.

The forecast is based on estimated parameters.

The parameters at time T are computed from the observation at time T and the previous m-1 observations:

Using these m observations, we find the linear equation that minimize thes sum of squares of the difference of the observations from the fitted line. The values of the indices, -k, are the independent variables for the simple regression. The values of the observations, 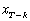, are the dependent variables. The following parameter estimates are based on the least squares normal equations for fitting a linear equation.

The forecast for the expected value for future periods is a constant plus a linear term that depends on the number of periods into the future.

With a trend estimate as part of the forecast, this method will track changes in trend. We use the same data as for the other forecasting methods. We repeat the data below. Recall that the simulated data begins with a constant mean of 10. At time 11 the mean increases with a trend of 1 until time 20 when the mean becomes a constant again with value 20. The noise is simulated using a normal distribution with mean 0 and standard deviation 3.

The estimates for three different values of m are shown together with the mean of the time series in the figure below. The figure shows the estimate of the mean at each time and not the forecast.

The estimate follows the trend line more closely than the moving average or exponential smoothing methods. During the times when the mean is constant, the regression estimate is more variable than the moving average method.

Forecasting with Excel

The Forecasting add-in implements the regression formulas. The example below shows the analysis provided by the add-in for the sample data in column B. The first 10 observations are indexed -9 through 0. Compared to the table above, the period indices are shifted by -10.

The first ten observations provide the startup values for the estimate. The constant and trend estimates are shown in columens C and D. The Fore(1) column (E) shows a forecast for one period into the future. The forecast interval is in cell D3. The regression parameter m is in cell C3. When the forecast interval is changed to a larger number the numbers in the Fore column are shifted down.

The Err(1) column (F) shows the error between the observation and the forecast. The standard deviation and Mean Average Deviation (MAD) are computed in cells F6 and F7 respectively.