|
|
The Dynamic Programming add-in provides the
structure on which the user can define a DP formulation. The
various model components are represented as Excel formulas
entered in the cells of the worksheet.
|
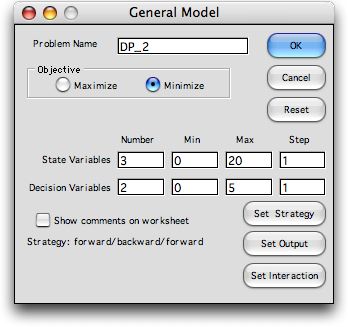
The General item on the
Teach DP menu constructs a Dynamic Programming
model with an arbitrary number of state
and decision variables. The dialog box
is shown below.
|
The model created by this dialog is very similar
to the knapsack model. The general model provides a structure
on which the student can construct DP models.
The model for a default problem is constructed
with the general model. This allows the solution procedures
to be demonstrated without additional data. For the one decision
variable case, the model is given below. The first term in
the objective reads: If the value of x is greater
than 0, the value of the term is 5, but if x is 0,
the value of the term is 0. Because of this fixed charge
there is a tendency to have a small number of x values
nonzero. This is contradicted, however, by the second term
which penalizes large values of x. The default problem
varies with the problem parameters.
|
Formulas for the Model |
| |
We use the knapsack problem is an instance of
a more general class of problems called Allocation of Scarce
Resources. We introduce the mathematical programming and dynamic
programming models for this class in this section. We use the
knapsack problem as an illustration of how the model is implemented
in Excel. By entering similar equations the student can implement
and solve any reasonably small discrete space dynamic programing
model.
The problem is to determine the optimum
investment level in each of n alternatives. The return
for each alternative is given as a function of its index and
the amount invested. The objective is to determine an investment
policy that maximizes the total return. For the knapsack problem,
the alternatives are the collection of items from which a selection
is to be made. The level of investment for item j is the
number of the items to bring.
|
| |
One or more resources are used up with the
decisions. In the case of the knapsack problem the single constraint
is the weight limitation.

|
| |
The objective function and constraints
comprise the mathematical programming statement of the allocation
of scarce resources problem. Since the decisions are required
to assume integer values, neither linear nor nonlinear programming
is an appropriate solution technique. An enumerative solution
procedure such as integer programming or dynamic programming
must be used. Dynamic programming is very general with regard
to the functional form the objective terms and constraint terms.
Linearity is not required. Although most problems that can be
solved by dynamic programming can also be solved with integer
programming, the integer programming model will usually be quite
large and complex if nonlinear functions are part of the situation. |
Dynamic Programming Model |
| |
To formulate this problem for dynamic
programming, a solution must be described as a sequence of states
and decisions. The sequence of decisions is easily obtained by
arbitrarily ordering the investment opportunities. Thus the first
decision is the level of investment in opportunity 1, the second
decision is the level for opportunity 2 and so on. To complete
the model we must define each of the model components listed
below. Many variations in the problem statement can be accommodated
by minor variations in the model.
In the following we describe the mathematical formulation of
the model together with the Excel implementation. The add-in
constructs a number of named ranges on a worksheet defining the
model. All the ranges are prefixed with the worksheet name, DP1_,
for this example. This allows a workbook to hold a number of
dynamic programming models, each with a unique name. In our descriptions
we will use the prefix DP1_ to explain the features of the model,
however, that prefix will differ for problems with other names. |
Options |
| |
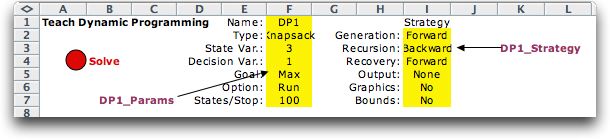
The program is governed by a number
of parameters that identify the type, dimensions and optimization
criterion of the model, control the solution strategy, and specify
the material that is displayed during and after a run. The program
constructs two named ranges, DP1_Param and DP1_Strategy, to hold
this information. They are indicated in yellow in the figure.
The first four entries in the Params range are set during the
problem definition. The other entries in the two arrays can be
changed by choosing the Options menu item from the Teach menu.
|
States |
| |
The dynamic process starts in an
initial state. After each decision the process moves to a different
state. Finally the process is finished when a final state is
reached. The state vector identifies the states of the process. |
| |
Mathematical Description

|
| |
Excel Definition |
| |
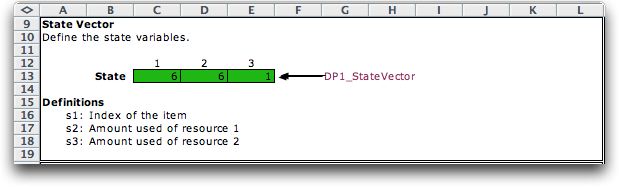
The Excel model uses the worksheet
region from row 9 to row 19 to hold state information. The definitions
of the states are in rows 16 through 18. The number of rows will
expand to accept the number of state variables. The array named
DP1_StateVector is used during the solution process to hold values
of the state variables.
|
Decisions |
| |
Mathematical Description |
| |
The vector of feasible decisions is defined by lower and
upper bounds on the decision variables. For the knapsack
problem, the decision is how many of an item to bring, so
the vector has only one component.
|
| |
Excel Definition
The decision vector and its bounds start at
row 20 of the worksheet. In row 23, we see the named range
DP1_StateDecVector. During computation this range will be
set equal to the values in the DP1_StateVector range defined
above. We do this because the feasibility conditions for
a decision might depend on the state definition. Formulas
implementing such a relationship can point to cells in the
DP1_StateDecVector range. Similar arrangements will be noted
for other components of the formulation.
The decision value is in row 25. If the decision
were a vector with more than one element, cells are provided
for each component. Below the decision value are cells for
the minimum, maximum and step size for each decision variable
(rows 27 through 29). During the solution process the decision
is taken through each possibility for every state. The limits
allow the values 0, 1, and 2 for the decision variable.
|
| |
|
| |
Excel Formulas
Row 26 holds equations that determine the feasibility of
the decision. Cell C26 contains a Boolean formula that returns
True if the first decision variable is between its bounds.
Cell D26 is true if all the decision variables are feasible.
The formulas that accomplish these computations are shown
in the Excel Formula view below. The formulas in both C26
and D26 use the AND Boolean function. In the latter case
the statement AND(DP1_DecLogic) is TRUE if all the cells
in the range DP1_DecLogic are TRUE.
We see in cells C23, C24, C25 the formulas that make these
cells equal to the cells in the DP1_StateVector range. These
formulas are added by the solution procedure, and need not
be a concern of the user.
Formulas in yellow cells are added by the computer when
necessary for the solution process. The formula in C25 accomplishes
the process of enumerating the set of decisions. The program
refers to DP1_DecInd, a number in cell B31. As that number
ranges from 0 to 3, the decision value in C25 ranges from
0 to 3. This isn't very exciting for this small case, but
the procedure is very powerful for enumerating all feasible
decisions for a decision vector with more than one variable.
The contents of cells C30, C31 and B31 are also used by
the program.
The important formulas for the user trying to implement
a different problem are those in C26 and D26. These can
be any Boolean functions or combinations of functions available
to Excel. Very complex feasibility conditions can be constructed.
|
|
|
Forward Transition Equations |
| |
The forward transition equations compute the state that
is reached by taking decision d while in state s.
For the knapsack problem the decision moves to the next
opportunity and increases the amounts used of each resource
by an amount that depends on the decision.
Mathematical Description
|
| |
|
| |
Excel Definition
We see below the Excel worksheet area implementing the
forward transition functions. The ranges DP1_StateForVector
and DP1_DecForVector copy the state and decision information
from the ranges in the upper part of the worksheet that
hold the state and decision vectors.
The range circled in red holds the next state. Although
in this case the program has filled this range with formulas
appropriate to the knapsack problem, the user can provide
his or her own formulas to implement any desired transition
functions.
|
| |
|
| |
Excel Formulas
The specific formulas for the knapsack problem are in row
43 in the figure below. The formula in C43 simply adds 1
to the contents of C39. C39 holds the index of the opportunity,
so cell C43 computes the index of the next opportunity.
Cells D43 and E43 compute the amount of resources for the
next state. The references to DP1_Res refers to the range
holding the resource usage amounts. The INDEX function is
helpful in that it chooses a number from a range for a given
row and column. Note that the unit resource is multiplied
by C40, and that cell holds the decision value.
Again, here is the place where the user will put new formulas
to describe the transition equations for different problems.
|
|
|
Decision Objective and Recursive
Equation |
| |
Mathematical Description
These functions comprise the objective function of dynamic
programming. The contribution of a decision d taken
while in state s is computed by the decision objective.
This can be a function of s, d, and s'
(the next state reached).
|
| |
|
| |
The backward recursive equation shows how the contribution
of a decision is combined with the results of the optimal
decisions starting from state s'. This is a recursive equation
because the value of f(s) depends on the value
of f(s').
|
| |
|
| |
Excel Definition
The two quantities to be computed are scalar quantities
and are each computed in a single cell of the worksheet.
The decision objective is in cell F53 and the backward
recursive equation is in cell C53. The value of the recursive
equation for the next state is placed by the add-in in
cell I53.
|
| |
|
| |
Excel Formulas
The decision objective for the example is in cell F53.
The unit benefits for the items are stored in DP1_Ben,
and the function multiplies the decision value times the
unit benefit.
The recursive equation is very simple in this case. The
Backward Recursive equation in C53 adds DP1_DecValue (cell
F53) to DP1_NextStateValue (cell I53). During the solution
process the computer puts appropriate values into DP1_NextStateValue
to solve the recursive equation.
|
|
|
Initial States |
| |
The sequential decision problem can begin at one or more
initial stats. When more than one is specified, the program
selects the one with the best objective.
Mathematical Description
For the knapsack, we consider only one starting state (1,
0, 0). That is, we start with opportunity 1 and no resources
used.
|
| |
|
| |
Excel Definition
The structure on the worksheet allows a number of feasible
initial states to be defined. In the present case, because
the minimum and maximum limits are equal, only one state,
(1,0,0), is an initial state.
|
| |
|
| |
Excel Formulas
The important formulas in this case are those that determine
the Boolean value in cell F60. If this cell is True, the
state in row 59 is an initial state, while if the cell
is False the state is not an initial state. For this example,
the state is judged initial if its components lie within
the bounds.
|
|
|
Final States |
| |
The decision process ends in a final state. Again, we use
sets to identify final states. For knapsack problem, a final
state has the first state variable equal to one greater
than the number of items.
Mathematical Description
|
| |
|
| |
Excel Definition
The structure for final states looks very much like that
for initial states. The state of cell F72 determines if
a given state (in row 71) is a final state.
|
| |
|
| |
|
|
|
State Feasibility |
| |
Dynamic programming solution algorithms need only consider
states that will lead to feasible final states. Infeasible
states are those that do not. The definition of feasible
states is important because the number of computations in
a DP solution is important to the number of states considered.
If some states can be eliminated because they are infeasible,
computational effort will be reduced.
Mathematical Description
Although in general quite complex conditions can be used
to define feasible states, in the example we use simple
bounds. The validity of these bounds depend on the fact
that all the resource usage coefficients are nonnegative.
Excel Definition
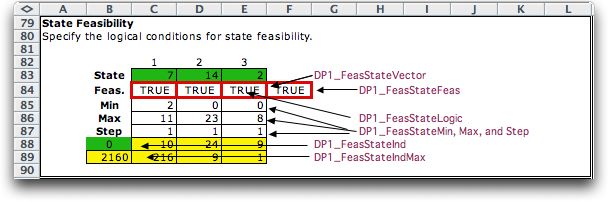
The feasibility conditions start in row 94. They are very
similar to the structures for initial and final states,
except the minimum and maximum limits are different. In
addition to the primarily function of identifying feasible
states in the solution process, the structure below is used
by the exhaustive enumeration procedure for state generation.
When the DP1_FeasStateInd is assigned all the integer values
in the range 0 to 5225, all the states will have been generated.
Formulas placed in row 98 determine the state values from
the enumeration index.
|
| |
Excel Formulas
|
|
|
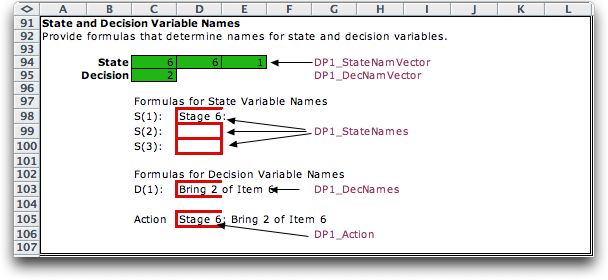
State and Decision Variable Names |
| |
Excel Definition
This area on the worksheet is not necessary for the DP
solution process, but it is very useful for presenting the
results of the DP solution in terms of actions. The cell
labeled DP1_Action is to hold a phrase that explains the
current state and decision. This cell is a concatenation
of the red bordered cells above. The latter cells have formulas
that generate string expressions.
|
| |
Excel Formulas
|
|
|
| |
|

