The second item on the Teach NLP menu presents the function dialog shown below. A function has a location, given by a cell address, and a name. The cell address is determined by the cursor placement on the worksheet when the dialog appears. The Function Location text field is locked, so have the cursor placed at the desired location when the menu item is selected. A function definition may take up a number of cells on the worksheet, so leave an appropriate amount of empty space below and to the right of the cursor location. The program gives a warning before the function overwrites cells that contain information.

In the Function Name field, the program presents one of nine preset names: F, G, H, J, K, L, M, N, and O. When these names have all been used, the letters are repeated, FF, GG, etc. When all the two letter pairs are generated, three letters are used. The student can change the suggested name. The name is used by the program to identify various regions on the worksheet.

Every function depends on cells on the worksheet that hold variable values. For this dialog, we expect that a decision vector has been previously defined using the Add Variable menu command. The name of the variable range is placed in the Decision Vector text box.

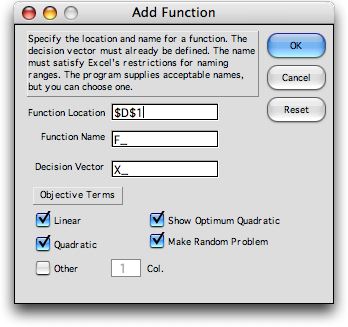
The check boxes in the lower half of the dialog, determine the data structure that is placed on the worksheet. The figure below shows the worksheet areas created by the dialog. The range D1:L6 is first cleared by the program. If cells in the range are not empty, the program gives a warning. If the student does not want the cells to be overwritten, he or she can cancel construction of the function and choose a new location.

The function name is placed at the top left cell of the region and the Excel formula computing the function is placed in the cell immediately below. The cell with the red text is given the Excel name that is the name of the function. In this case cell D2 has the name F. The remainder of the range defines data and results areas.

The second column, column E, names the decision variable and provides indices for the linear coefficient vector. The third column is for the linear coefficients of the function. The values in the range F2:F5 were assigned randomly for this case. They can of course be changed. At the bottom of the column, the matrix product cx is computed. Cell F6 is colored yellow to indicate that it contains a formula. Although areas colored yellow may be changed by the student, changes should be done very carefully.

Column G begins the presentation of the Q matrix that holds the coefficients for the quadratic terms of the function. The coefficients are stored in the range H2:K5. Cell H6 holds the result of the matrix computation: 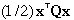, which is the contribution of the quadratic terms to the objective function. The range L2:L5 holds the results of the computation Qx. These results are necessary for computing the number in H6. The value in cell D2 is the sum of the linear and quadratic computations. The value depends on the contents of the decision variable X. The numbers in the variable range B2:B5 are arbitrarily entered for this illustration.

When the function has only linear and quadratic terms, the stationary point of the function can be analytically determined as the matrix expression . The usual expression for the point is , but we have shown the c vector as a column vector rather than a row vector. In this case the stationary point in the range M2:M 5, is a global minimum. In numeric tests of the direct search algorithms, it is interesting to compare the numeric solution with the analytic optimum.

It is tempting for the student to copy the optimum solution in column M and paste it in the range of the X vector in column B. The entries for X* are computed with an Excel array expression. To transfer the values, first copy the range M2:M5. Then Paste Special:Values into B2:B5. If you simply Paste into B2:B5 the array formula will be transferred. When the computer attempts to vary the contents of the X vector, an error will be generated because Excel does not allow individual cells of a array computation to be changed.

Other Terms

A second example is below. Here the Other box in the dialog has been checked with 2 columns designated.

The Other Terms column can hold any legitimate Excel functions (restrictions on the functions that can be used are described in a later section). The second column is for numbers used by the functions. These columns are for the convenience of the user. Many situations require a separable function of the decision variables. Such terms are conveniently entered in the Other Terms column.

Single Cell

The simplest definition of a function has no boxes checked on the dialog.

The function L(Y) in the example below uses only a 2x2 range of cells. The function defining L(Y) is in cell A14. Actually, the function definition may use data and formulae outside the defined ranges. It is only required that the contents of the function cell, A14 in this case, depend in a deterministic way on the contents of the cells holding the decision variables, B9:B10. Excel offers a practically limitless variety of functional forms.

It is important to note that this program requires that all the formulas and constants affecting a particular functional value be placed on the same worksheet.