Optimize Dialog

Selecting the menu item presents the Optimize dialog illustrated below. The top three fields are RefEdit fields. These allow the user to specify ranges on the worksheet by selecting them with the cursor. We prefer that the the student enter the contents of these fields as described in this section, but the RefEdit fields offer flexibility that will sometimes be useful.

The top field on the dialog holds the address of the worksheet cell where the results of the procedure will be presented. Again, this is the cell at the top left corner of a range that may extend considerably to the right and below the cell. The program will issue a warning if parts of the worksheet are to be overwritten. The default contents of the Results Location field is the address of the current cursor location. For this dialog, the field is not locked. A different address can be entered manually, or the RefEdit field allows the user to point to the desired location with the cursor.

The Objective Cell holds the name of the function to be optimized. The Variable Range holds the name of the decision variable. Of course, these names must have previously been defined through the Add Function and Add Variable menu items.

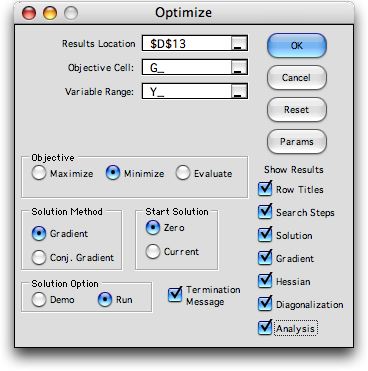
The remainder of the dialog holds various options. The Objective frame determines the direction of optimization. In addition to Maximize and Minimize, we include the Evaluate button. With this option, the program evaluates the point currently specified in the Y vector.

The Solution Method frame shows the two methods currently available. In this section we are discussing the Gradient direct search method. The Start Solution frame indicates whether the procedure is to start from a zero vector or from the current value of the Y vector. Two solution options are provided. In the Demo option, the program stops at each step with a description of the current activities of the algorithm. This is useful for instruction. The Run option goes through the steps of the algorithm without interruption.

The results presented by the program are determined by the several check boxes on the dialog. They will be illustrated through the examples on this page.

Search Parameters

The Params button allows the user to specify stopping criteria and other parameters for the direct search methods. Direct search algorithms for nonlinear programming actually look for the optimum with intelligent trial and error. There are no conditions that identify the optimum exactly, rather we specify a set of termination criteria that indicate that the program may be close to the optimum. Pressing the Params button presents the dialog below.

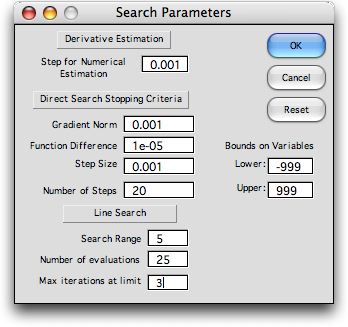
Here we define the various terms on the dialog. Most of the entries on the dialog are stopping criteria for the direct search procedure. Whenever the program reaches a point that satisfies one of these criteria, it stops. If the Termination Message option has been chosen, the user can then change the criteria and allow the search process to continue.

Derivative Estimation

• Step for Numerical Estimation of Derivatives: First and second derivatives are estimated by finite difference methods that compute the function for slightly different values of the decision variables. This is difference between successive values.

Direct Search Stopping Criteria

• Gradient Norm: The gradient is the vector of first derivatives. It's norm is the magnitude of the gradient vector. One expects this number to be small near the optimum. When the gradient norm gets smaller than this limit, the program stops and identifies the point as a stationary point.
• Function Difference: Near the optimum, the difference between successive values of the objective function will become small. When the difference is smaller than this number, the program stops.
• Step Size: At each iteration of a direct search method, a step is taken in some search direction that will improve the objective function. Near the optimum, one expects this step to become smaller and smaller. When the magnitude of the step falls below the limit specified here, the program stops.
• Number of Steps: At this number of steps, the program will stop.

Line Search

• Search Range: The program uses a Golden Section line search procedure to find the optimum point along a search direction. The search direction is given by a vector. The length of the step is the magnitude of the direction vector multiplied by the number determined by the Golden Section. This parameter is the maximum of the latter. In cases where the direction vector is normalized, as for the gradient search, the search range gives the length of the maximum search step.
• Number of Evaluations: This is the number of steps taken by the golden section method. The default value, 25, gives a range of uncertainty at termination of around 10 raised to the -5 power. This is a very small number.
• Max Iterations at Limit: When the step size is at the maximum step value 3 times in a row, the program suspects that the optimum may be unbounded. The program then stops.

Bounds on Variables

• When a component of the search vector goes outside the range specified here, the program judges that the optimum may be unbounded. The program warns the student and provides an opportunity to terminate.

Direct Search with the Gradient Method

The OK button initiates the direct search procedure. If the Search Steps output option has been chosen, the progress of the search will be displayed as below. The example is the G(Y) function defined earlier. The starting point is the zero value of the decision vector. At each step we see a yellow area showing the value of the objective function, outlined in red, and the values of the decision variables.

The green areas show the direction vector, D(k). For the gradient search, the search direction is proportional to the gradient. For minimization the search goes in the negative direction of the gradient, and for maximization the search goes in the positive direction. We have normalized the gradient vector so that its magnitude is 1. The yellow area below the direction vector is the length of the step that minimizes the objective function in the search direction. The number below the yellow area is the number of function evaluations necessary for the search. In this case the number is 29, the number of iterations of the golden section search plus the 4 necessary to numerically estimate the gradient.

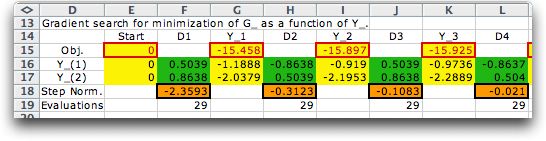
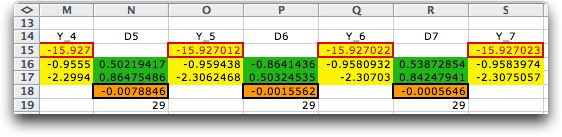
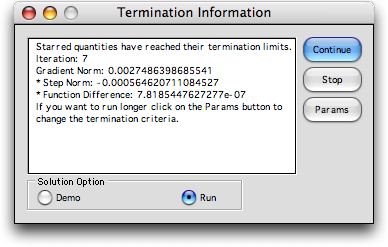
When the Termination Message box is checked, the program stops when one of the stopping criteria is met. The program presents a summary of the current results and allows the user to change the criteria. In this case, we select Stop and the final results are presented.

The extent of the results depends on the options checked on the Optimization dialog. For the example, all the options were chosen. The Row Titles option prints the contents of column D. For some applications, we might what a series of solutions for different problem parameters. For a better presentation, show the titles only with the first run. The Solution option shows the solution shown in column E. The Gradient Option shows the gradient vector for the variable values of the current solution. The Hessian matrix is the matrix of second derivatives. With that option chosen the program numerically estimates the Hessian matrix, shown for the example in columns G and H. The Diagonalization option, transforms the Hessian to obtain a diagonal matrix. This matrix is used for the analysis.

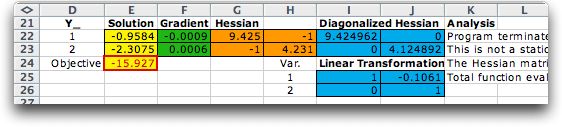
The Analysis option presents information about the search process. The first line for the example shows the termination mechanism. The second line shows the current magnitude of the gradient vector. The value does not fall below the limit of 0.001 specified in the parameter list, so the point is judged to be not a stationary point. The diagonalization is used to determine the character of the Hessian matrix. In this case it is positive definite, indicating that the function is convex at this point. For a stationary point this would indicate a local minimum. Including the numerical estimates of the gradient and Hessian matrices necessary for the final analysis, the process required 217 evaluations of the G function. This measure can be used to compare different search strategies.