| The Mixed Integer Programming
contains some variables that are integer and some that are continuous.
In the following we define n variables to be integer
and n' variables to be continuous. We use y
for the continuous variables and place primes on the parameters
for the continuous variables. For convenience we show all the
constraints as "less than or equal to" inequalities,
however, slight modifications handle all three allowed constraint
types.
Mixed IP Model: MIP

|
To obtain the COP representation, we first change the model
into two parts, one for the integer variables and one for the
continuous variables.
The integer problem has a term in the
objective that is the optimum value of the linear program
formed by the continuous variables.
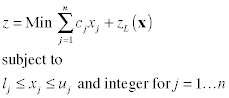
The linear problem depends on the integer
solution. We have changed the constraints to equalities
by adding slack variables that allow both positive and
negative deviations from the right side. This model
has a feasible solution for all x,
but solutions that violate the original constraints
are penalized.
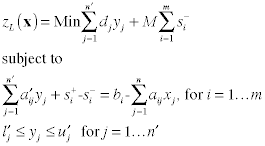
|
The COP model for the MIP includes the objective for the continuous
problem as a term in the objective. Constraints are included
in the continuous problem, so are only explicitly considered
in the COP.
Mixed IP COP Model: MIP-COP
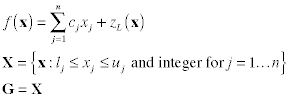
|
There are methods for solving the MIP directly using branch
and bound or cutting planes, so one might ask, why do we change
it to a COP? The COP approach is reasonable if there are not
too many integer variables, or some feature of the continuous
model makes it easy to solve. For problems with small n,
using the enumerative methods of COP allows one to use only
an LP rather than a specialized MIP algorithm. For other problems,
the continuous problem may be easy to solve. This is particularly
true if the LP has the form of one the easy problems, such as
the min-cost flow or assignment problems.
The Optimize discussion includes illustrations where
the method is used for MIP
and the fixed
charge network design problem using either a min-cost flow
or transportation model for the continuous part of the problem. |

