|
|
|
|
Combinatorial
Optimization
|

|
Permutation
Problem |
| |
Several problems are
solved by finding an optimum permutation of the first n
integers. As an example consider the simple assignment problem.
There are n tasks and n machines. A cost is
specified for completing each task with each machine. The problem
is to assign one task to each machine so that all tasks are
completed with the smallest total cost. This is a combinatorial
problem whose solution is described by a permutation of n
integers. For a seven task problem one solution is given by
the permutation: (1, 2, 3, 4, 5, 6, 7). This implies assigning
task 1 to machine 1, task 2 to machine 2 and so on. Every permutation
describes an assignment.
The linear assignment problem just described is one of the
simplest of the combinatorial problems and can be solved with
linear programming as well as with several special purpose algorithms.
Here we formulate and solve the problem as a combinatorial search
problem. Although this is a poor choice from a computational
point of view, it serves to illustrate the features of permutation
problems. There are a number of problems whose solution is a
permutation that that are not so easy to solve including the
quadratic
assignment problem and the facility
location problem. These problems are solved in the Combinatorial
add-in and the Layout add-in with procedures that call
the permutation option of this Optimize
add-in.
We state the general permutation combinatorial model in terms
of assigning n machines to n tasks.
Permutation Problem: Permute-COP

The solution x is a permutation
if all of the components of x have
different values.
|
The general model allows any objective function or constraint
set. For the linear assignment problem a cost is given for each
machine-task assignment and the objective is to find the permutation
that minimizes the sum of the assignment costs. In the following
we assume all assignments are feasible.
|
Excel Model |
| |
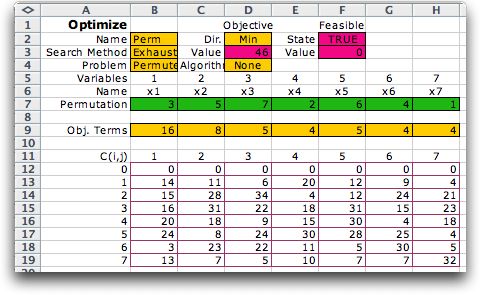
The general Permute-COP is implemented
in the Optimize
add-in. The figure below shows the model form for the linear
assignment problem. Exhaustive enumeration was used to obtain
the optimum solution for this seven task case. The matrix of
assignment costs is in range B12:H19. The solution vector is
in range B7:H7. The costs of the selected assignments are indicated
in B9:H9. The objective in D3 is the sum of the numbers in B9:H9. |
| 
|
| |
In terms of the model notation
the solution is:
It is interesting to observe how the integer programming model
for the assignment problem is different from the combinatorial
model. The assignment problem is written as an IP below. It
also has a pure network
flow model.
When the integrality constraints are neglected and the model
is solved with an LP algorithm, the solution turns out to be
integer. This fortunate event occurs because the constraint
matrix has the total unimodularity property. This property
assures that every extreme point of the feasible region of the
LP, and hence the optimal extreme point, has all integer values.
The math programming models for the transportation,
maximum
flow, shortest
path and pure
min-cost flow problems also have this characteristic. These
are combinatorial problems that are easy to solve. Why create
a COP model for them?
One reason is that the COP model is simpler. The IP has 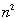 0-1 variables and 2n constraints where the combinatorial
model only has n variables and no constraints. A solution
described by a permutation automatically satisfies the requirements
that all machines are assigned and all tasks are performed.
0-1 variables and 2n constraints where the combinatorial
model only has n variables and no constraints. A solution
described by a permutation automatically satisfies the requirements
that all machines are assigned and all tasks are performed.
Another reason for the COP model is that it can handle a broader
range of assumptions. If one adds logical constraints to the
IP model, the solution of the LP relaxation may no longer be
integer and an IP algorithm such as branch and bound is necessary.
A nonlinear objective function results in an integer-nonlinear
model. Mild changes in the situation change the problem from
easy to hard. This is illustrated in the next section.
|
Quadratic Assignment Problem
|
| |
The quadratic assignment problem
(QAP) illustrates a combinatorial problem with a nonlinear objective
function. The mathematical model has the form of a linear assignment
problem, but the objective function is a quadratic function
of the variables. We describe the problem in terms of assigning
n departments to n locations. Data describes
the flow between every pair of departments with f(i,
j) the flow from i to j. The distance
between locations k and l is given as d(k,
l) for all location pairs k and l.
The QAP combinatorial model for assigning n locations
to n departments is the same as the Permute-COP with
some terms redefined.
Quadratic Assignment Problem: QAP-COP

The solution x is a permutation
if none of the components of x have
the same value.
|
The instance of the QAP that represents the location problem
has the objective defined below. Notice that the variables appear
as indices of the distance matrix.
The mathematical programming model for the QAP has the same
constraints as the linear assignment problem, but a much more
complicated objective. This is a very difficult problem to solve
and there are a number of papers about solving the QAP. Although
there are still 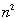 variables,
there are variables,
there are 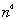 nonlinear terms in the objective function.
nonlinear terms in the objective function.
The Combinatorics
add-in builds a model for the QAP and solves the problem
as a permutation COP. The Layout
add-in has an option to solve certain facility layout problems
as QAP.
|
|
| |
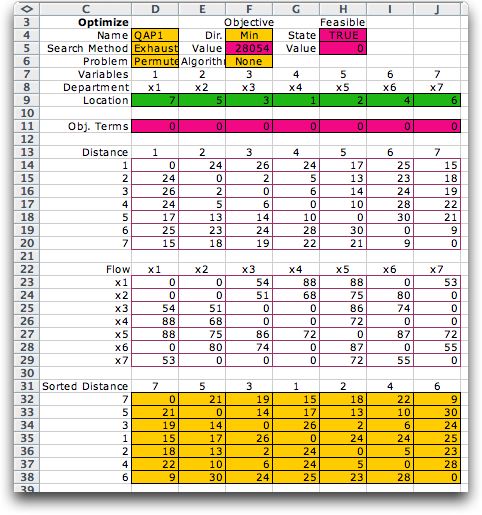
The QAP model constructed by the
Combinatorics
add-in for a seven department problem is shown below. The assignment
is in D9:J9. The distance matrix is in D14:J20 and the Flow
matrix is in D23:J29. A critical part of the Excel model is
the Sorted Distance matrix in D32:J38. This matrix
is created with Excel equations, and the matrix changes with
the assignment. The objective function value is computed in
F5 with a simple SUMPRODUCT function.
Although the exhaustive enumeration approach used
to solve this example is not practical for larger problems,
partial enumeration methods are available that offer a good
chance of finding a satisfactory, if not optimum, solution.
The combinatorial description described on this
page is very general and the methods can be used for a variety
of problems. Excel is primarily an evaluation tool and very
complex models can be built to evaluate specific solutions.
Unless great care is take by a skilled analyst an Excel model
is unlikely to have the form necessary for solution by an algorithm
specialized to a particular set of problems. The combinatorial
approach is available for most models. |
| |
|
|
|

