| |
The Markov decision process, MDP,
model for the birth-death process adds decisions to the DTMC.
Rather that purging only when the system is full, the model
allows purging to occur at any population other than 0. An
example of a situation addressed by this model is to find the
optimum batch size for a process that treats the entire batch
at once. Say a car repair shop has a van for transporting customers
to their homes. During the morning hours customers arrive to
the van at a constant average rate, but the time between arrivals
has an exponential distributions. Customers wait until the
van is ready to go. The driver leaves the shop when the number
of waiting customers reaches some prespecified limit. All waiting
customers are handled in a single trip. While the van is gone,
customers again start gathering for the next trip. We neglect
the complexities that arise because of the time required the
van to make its trip and assume that a van is always available.
Although the example depends on arrivals we also allow the
customers to leave without using the van.
|
| |
 |
This MDP data form
has two more items than the DTMC. The new items reduce
the size of the optimization problem. The Minimum
Population to allow Purge
prohibits the purge decision when the population is below this
value. The Maximum Population to Accept forces the purge
operation for populations greater than this value.
The MDP model requires a dynamic programming solution approach
provided by the DP Solver add-in. |
Model Elements |
 |
Clicking the Build
Model button creates a new worksheet holding the model
and fills the model with the data and formulas describing
the birth-death process. The model
worksheet is discussed on the DP
Model pages. The MDP model has three elements,
states, actions and events. |
| |
 |
The model has a single state variable specifying
the population. The yellow cells outlined in red hold formulas
linking the cell contents to items on the data worksheet.
For example, the entry in cell F19 has a formula that links
to the Maximum Population on the data sheet. Changing
the data automatically changes this
cell. |
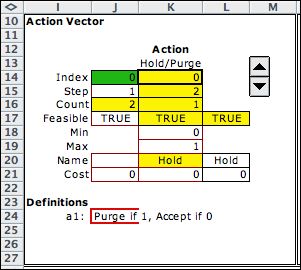 |
The action has two possibilities indicated by the contents
of cell K14. The value of 0 indicates that decision is to Hold the
purge decision until later. A value of 0 means that the Purge decision
is accepted for the current state. |
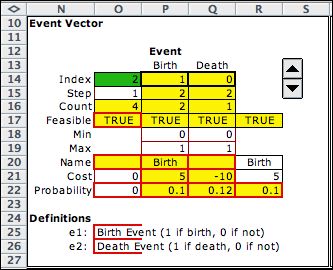 |
The events driving the system are births and deaths. The
current event is shown by the two dimensional vector in row
14. For the model, the feasibility condition in cell O17
returns TRUE only when the event vector is (1,0) or (0,1).
Costs and probabilities of the events are transferred from
the data. |
|
Decisions |
| |
The decisions of the
model describe state/action combinations that are feasible. The
birth-death model has three decision sets. The first indicates
that only the action Hold is available for populations
between 0 and 4. The second decision allows both the hold and
purge actions for states 5 through 9. The third allows only the
purge option when the state is at the maximum population. The
sets in this case are mutually exclusive. |
| |
|
Transitions |
| |
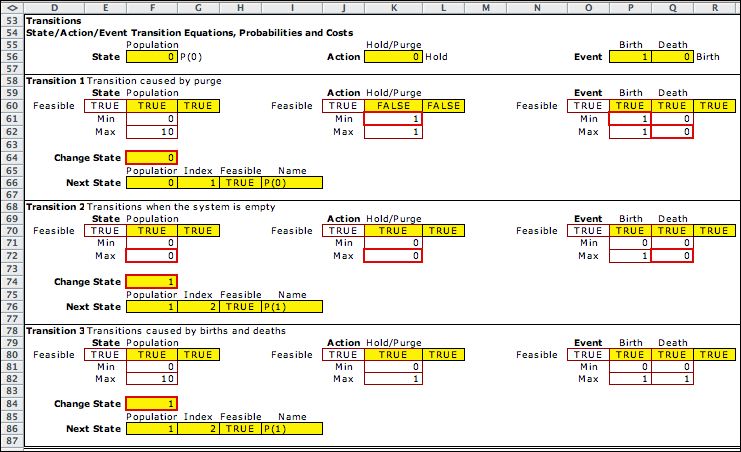
Given a state and an
action, an event causes a transition. The transition sets are
shown in the figure below. The different transition sets describe
different state/action/event combinations that determine the
transition. The second transition block is controlling for state
0, the hold action and the arrival event. The
transition determines that the next state will have a population
of 1. The
sets need not be mutually exclusive. If a transition falls into
more than one set, the one nearest the top of the list is accepted. |
 |
Enumeration |
| |
The model describes the
situation in concise terms. To provide a model for the solver,
the program enumerates the elements of the model through all
possibilities. The lists below are created. |
| |
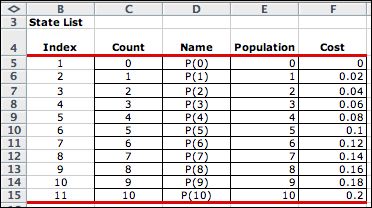
The State List
|
| |
The
Action List

|
| |
The
Event List

|
| |
The decision list combines
all feasible states with all feasible actions. A decision is
feasible if it falls in one of three decision sets.
The Decision List

|
| |
The transition list
combines all feasible decisions with all feasible events.
A transition is included if it falls in one of three transition
sets. A transition determines the transition cost, transition
probabilities and the next state. The model does not explicitly
define the Null event. For each decision, the transition
probabilities must sum to 1. If the model defines transitions
with a probability sum less than 1, the remaining probability
is assigned to a Null event.
The Transition List

:

|
Solution |
| |
The lists are used by
the DP Solver algorithms to find an optimal solution to the decision
problem. The figure shows the decision solution in rows J (by
index) and K (by name). The optimum policy is to purge when the
system reaches the population of 9 or 10. Column N shows the
net present worth vector for an unlimited time horizon. For example,
if the system starts with a population of 0, the net present
worth of the costs for operating the system with the optimum
policy is -435.508. The negative value means that
the system provides a net profit. Column O shows the steady-state
probability vector when the optimum policy is followed. The probability
for the population 10 is very small because it is a transient
state. When the system starts at some population other than 10,
the process never reaches it. |
|
| |
There is much more to
the DP Solver worksheet than shown in the figure. The entire
worksheet is discussed on the DP Solver pages. |
Summary |
| |
We provide three models
based on the birth-death process. The Markov Chain models are
for the DTMC and the CTMC. Both can be solved with the Markov
Analysis add-in. The DTMC can also be solved with the DP Solver
add-in. The MDP model is an extension of the DTMC that allows
decisions at each state. It can only be solved using he DP
Solver.
|
| |
|



