 |
The CTMC data is quite similar
to the DTMC except that a step size is not specified and values
that depend on the step size are not computed. The cell formerly
holding the step size now holds a parameter called mean
lead time. The lead time is the time between when a replenishment
order is placed and when the order quantity is delivered into
inventory. The other models assume a fixed lead time of one
step, 0.5 weeks in our example. For the CTMC the lead time
is a random variable that has an exponential distribution with
a mean of 0.5 weeks.
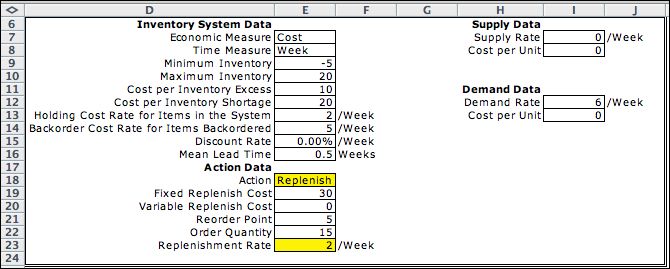
For the CTMC all the event components are random
variables with exponential distributions. This is consistent
with the demand over a finite interval having a Poisson distribution,
as assumed by the other models. Time is continuous and a transition
occurs only when an event occurs. Two or more events
cannot occur at the same time. In the inventory model there
are only three event components: an arrival when a unit of
supply arrives, a departure when a unit of demand arrives,
and a replenishment when the lot (or order quantity) is delivered.
Since the supply rate for the example is 0, the supply event
never occurs. The demand rate is 6 per week, so the mean time
between demand events is 1/6. The mean replenishment time
is 0.5 weeks, so the mean replenishment rate is 2 per week. |
The Model |
|
The model for the CTMC is quite
different than the models using the fixed step size. The state
variable now has two dimensions. The first state variable is
the stock level. The second state variable is binary. The value
of 1 indicates that a replenishment order has been placed and
the value of 0 indicates that no order is outstanding.
The event has three components, one for supply, one for demand,
and one for replenishment. Each has two possibilities, 0 and
1. The value 1 indicates that the associated event
has occurred, while a 0 indicates that it has not. The feasibility
cell K17 has a logical expression:
=SUM(CTMC_DPM_Event)=1
This means that exactly one of the components is equal to
1 when an event occurs. The example shows the occurrence
of the demand event. The current stock level is 3 and a replenishment
order is outstanding. |
|
| |
An event signals a transition, and the transition
blocks determine the new state, the cost of transition and
the rate of transition. The first block represents the delivery
of a replenishment order. This transition is possible
only when there is an outstanding order (the second state variable
is 1) and the event indicates a replenishment.
The second transition describes the process of placing an
order. An order is placed whenever there is no outstanding
order and the stock level is less than or equal to the reorder
point (5 for the example).
The third transition describes a simple unit supply or demand.
This transition is feasible for the given state and event and
the transition prescribes a transition to state (2, 1). The
rate of the transition is 6 and its cost is 0. |
|
Lists |
| |
The enumeration process creates the state
list, event list and transition list. |
| |
|
The state list is generated by
sequencing all possible values of the state counter E14.
There are 52 states with the parameters specified on the
Data worksheet. |
|
| |
|
The event list has only three
entries. |
|
| |
|
When all feasible states are
enumerated with all feasible events, 72 transitions are
discovered. Transitions with 0 rate are not listed and
we see no events with supply. |
|
Markov Analysis |
| |
|
The Markov Analysis add-in
is the only solution alternative for the CTMC. On transferring
the lists to that program we find that many of the states
are transient for the data parameters given.
A variety of analyses are possible with the add-in, but
there are too many states to obtain steady-state results. |
|
Summary |
| |
The CTMC model is interesting because it is
so different than the DTMC model. It includes a state variable
indicating whether a replenishment has been ordered. This suggests
a way to handle a fixed lead time (other than 1) in the other
models. The new model would have a state variable that counts
the number of steps since the replenishment order. When that
state variable reaches the lead time, the replenishment would
be delivered. We leave this as an exercise for the student. |
| |
|



