In this method, the relaxed master problem is solved to find feasible values of x, z and . This provides a lower bound as above. Using the values of z obtained we solve the subproblem. The solution provides an upper bound and also an extreme point of the subproblem. We add the associated cut to the relaxed master. The process continues until the lower and upper bounds are equal or sufficiently close together.

Step 0.	Solve the master problem with not included. The solution provides the initial upper bound.
Step 1	With the solution z from the master problem, solve the subproblem. If the solution to the master and the optimum solution to the subproblem, provides a better upper bound, replace the bound and the incumbent solution. The solution to the subproblem provides a new optimality cut.
Step 2	Add the optimality cut to the master problem and solve it. The value of the objective provides a better lower bound.
Step 3	If the difference between upper and lower bounds is less than some tolerance the stop. If the difference is zero, the optimum has been found. If it is not zero, then report the incumbent solution. If the bounds are not within the specified tolerance return to step 1 for another iteration.

Independent Subproblems

The L-shaped method is most effective if the submodel consists of a number of independent subproblems. This is the type of model provided by our side-model construction. The term in the objective of the master problem is the weighted sum of objective values, one for each subproblem. The individual subproblems each have a dual. They are independent except they all are affected by z and they all have the same constraint matrix W. Note that our notation has the dual variables and parameter matrices subscripted with the subproblem number.

Optimality cuts at each step are computed by combining the dual variables from the subproblems. The subproblem variables are shown with two subscripts, the first for the subproblem and the second for the iteration number for the L-shaped method. In the expressions below the variables are at their optimum values. The alternative RHS expression is valid when the subproblem variables have simple upper bounds.

Modifications for the Side Model

The side-model construction has several features and limitations not considered above. The Jensen LP/IP add-in modifies the method to accommodate side models constructed by the Math Programming add-in.

One useful feature is the inclusion of simple upper bounds for the subproblem variables. The development does not strictly hold with simple upper bounds unless they are explicitly included as constraints. The method uses the alternative RHS computation that does not explicitly mention the subproblem constraint set.

The side-model allows only limited variation of the linking variable constraint coefficients. The model uses a fixed matrix T multiplied by diagonal matrices that may vary by subproblem. Although this is limiting, a number of interesting cases can be handled as illustrated by the examples in this section and in the section on stochastic programming.

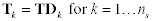
Objective functions may be maximized as well as minimized. The optimality cuts change direction.

Although the side-model allows nonlinear objective functions and integer variables, these features are not allowed for the L-shaped method. Integer variables violate the condition for the convexity of 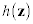. Although nonlinear objective functions may be convex, the Jensen LP/IP Solver cannot optimize nonlinear functions. The master problem can include integer variables, but the solution time for the branch and bound method may increase because of the added burden of solving the side model.

An important limitation is that the side models must be feasible for every z encountered by the method. This can only be guaranteed if the subproblems are feasible for every feasible solution of the master problem. One can always express subproblems in a way that satisfies this condition. The add-in stops whenever an infeasible subproblem solution is encountered. Infeasibility of the master problem will be discovered at the first step of the process. Optimality cuts cannot make the master problem infeasible.

For practical problems, the subproblems of a side model often have the same or similar optimal solutions with respect to the set of basic variables. After the first subproblem, the add-in includes a hot-start procedure that uses the basis obtained in the previous subproblem as the initial basis in the simplex method. When the basis is infeasible, a phase 1 procedure returns the solution to feasibility. For most problems this method reduces considerably the total number of simplex iterations required. At this time, the add-in does not use an advanced start method for the master problem.

The add-in has a feature that allows optimality constraints to be dropped after they become no longer binding to the master problem. Although this makes the master problem easier to solve, the lower bound may not decrease at each iteration and the method may not terminate.

Although limited, the provision of side models and the L-shaped method increases markedly the capability of the add-ins for math programming. A problem with a small master problem and many small subproblems may have thousands of variables and constraints when solved as a single combined problem. The problem would be far outside the capabilities of the free Excel Solver and the Jensen add-ins. When solved sequentially with the L-shaped method such problems are approachable with the Jensen LP/IP Solver.