When the distribution of a random variable is continuous rather than discrete, we will approximate the distribution with either a discrete distribution or a piece-wise uniform distribution. In this section we deal with the discrete approximation. We will illustrate this application with a simple-recourse model of the LP situation used at the beginning of this section.

To approximate the continuous distribution we select K+1 quantile values ranging from 0 to 1.

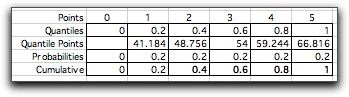
To illustrate, consider a Normal distribution with mean 54 and standard deviation 10. We divide the probability range into five intervals using the quantiles: 0, 0.2, 0.4, 0.6, 0.8, 1. The quantile points are computed with the RV_Inverse function of the Random Variables add-in.

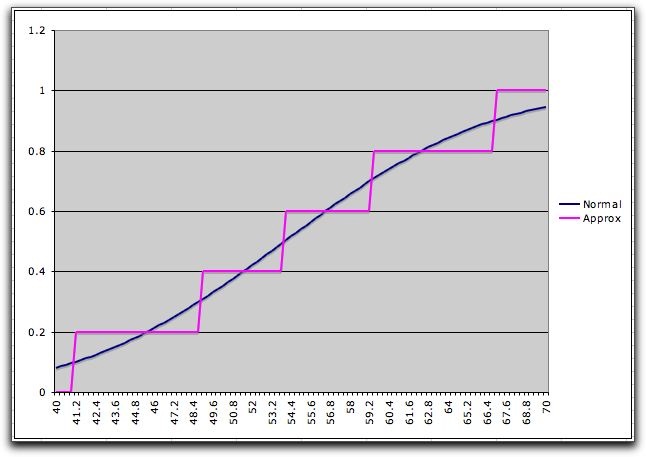
The graph below shows the cumulative distribution of this discrete approximation along with the Normal distribution. The construction of the graph shows the steps as ramps, but the steps are immediate at the quantile points. The approximation sometimes over estimates the continuous cumulative and sometimes underestimates it.

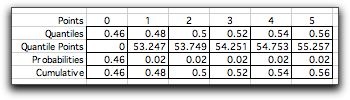
The number of steps and the selection of the quantiles controls the accuracy of the approximation. The table below shows a selection of quantiles that emphasizes the range 0.46 through 0.56.

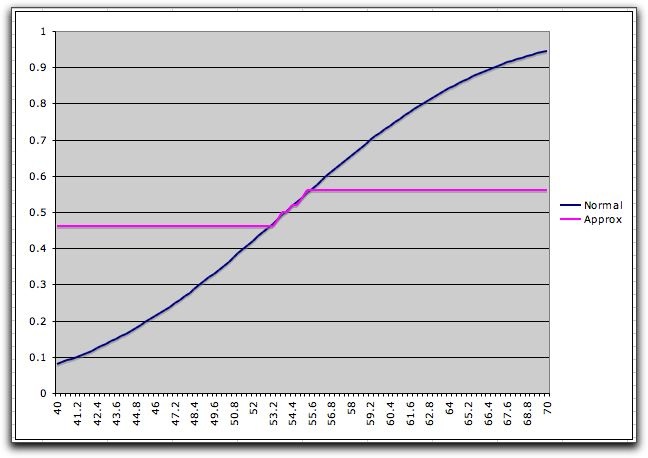
The cumulative distribution is more accurately represented in this range, while it is not well approximated outside the range. This feature will have usefulness for the simple recourse model.

Simple Recourse

We return to the ten product mix problem considered earlier, but now we will solve it as a simple-recourse model. The master problem below includes the production variables and the variables computing the resource usage.

To the right of the model we have constructed tables to compute the necessary probabilities and quantile points from the quantile values specified by the modeler. Normal distributions are defined in columns Y through AA. All computations relating to these distributions are provided by functions in the Random Variables add-in. Other distributions could just have well been used.

The piecewise linear representation of the expected recourse costs are expressed in the side model. We show the model in two parts below. The first part identifies the linking variables through the indices in row 29. Columns J through O provide information on T and D. The variables and the associated W matrix is in columns P through V. For definitions of the matrix terms, see the side model discussion.

The upper bounds defining the piecewise approximation are in columns W through AB. The associated objective coefficients are in AC through AH. The constraints in AK require the equality between the linking variables and the pieces.

Solution

Clicking the Solve button provides the solution shown below. The resource usage is seen in both the master and subproblems. The values of the subproblem variables, the green cells in the subproblems, shows the results for the pieces of the piecewise linear form.

The dual variables for the subproblem constraints can be found from a sensitivity analysis provided by the Solver. They are shown below adjacent to the table showing the approximation. The dual variables estimate the value of cumulative probability at the optimum solution, so the inverse of the probability estimates the optimum resource level. These are shown in column AI and roughly equal the values obtained for the optimum.

A Better Approximation

Based on the solution found with the rough approximations for the Normal distributions, we modify the quantiles under consideration to cover a smaller range of probabilities. In the table below we define five intervals in a 0.1 range for each random variable. The dual values shown and the resultant inverse probabilities are from the optimum solution.

The optimum solution is shown below for the revised quantiles. The value of the expected recourse cost is quite distorted by the approximation, so the optimum objective function is markedly different for this solution. The approximation adds a negative constant to all solutions, so the decision values obtained are the optimum for the more accurate representation. The slopes of the terms of the objective function of the LP determine the optimal solution, and the slopes in the smaller range are much more accurate than with the first approximation. The two solutions are compared in the table.

The dual solution provides an interesting interpretation. The dual indicates the risk that each constraint will be violated when the optimum solution is pursued. Clearly the last constraint, indicated by M5, is the most important constraint. The solution will have a shortage with respect to this RHS in over 95% of the future scenarios. Apparently, the profit obtained by using more of this resource is sufficient to pay for the cost of its violation. Of course the optimum solution and the risks depend on the penalties.