|
|
 |
Simulation |
 |
-
Production Model |
 |
The production model is adapted
from a story in The Goal by Goldratt. We first describe
the story and then use the add-in to model the more general
sequential production process. The story involves three boy
scouts playing with matches. The game involves throwing dice
and passing matches from one boy to the next. The scoutmaster
is at the end of the line trying to light a fire with the matches
produced by the third boy.
We start with a big pile of matches
to the left of the first boy. Boy 1 throws a single die. The
number showing is his production, so in this case the first
boy produces 4 matches. These matches are the raw materials
for the second boy.
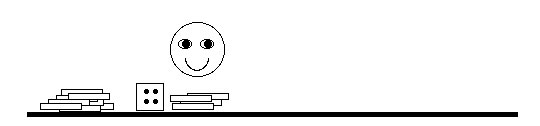
The second boy throws the die. His production capability is
the amount shown on the die, but he can only produce as much
as available from the first boy. His production is the minimum
of his capability or the number remaining from the first boy.
There are 4 matches available, but the capacity of the second
boy is only 2. He passes these to the third boy, leaving 2
matches remaining. These two are called
work in progress (WIP).
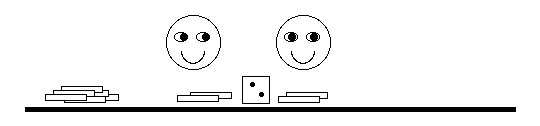
The raw materials for the third boy are the matches provided
by the second boy. Again, he produces the minimum on his die
or the matches available. For this case the capacity of the
third boy is 5, but only 2 matches are available as raw material.
The remaining 3 units of capacity are wasted. This is disappointing
to the third boy because his capacity was so much greater than
his production. There is no additional WIP.
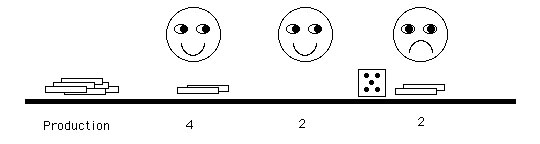
The scoutmaster has a demand that also depends on the throw
of the die. For the first iteration, the scoutmaster demands
4 matches. The third boy has only produced 2, so the scoutmaster
takes these two. The unsatisfied demand is lost. The
scoutmaster is disappointed with the third boy who seems to
be the bottleneck in this system.
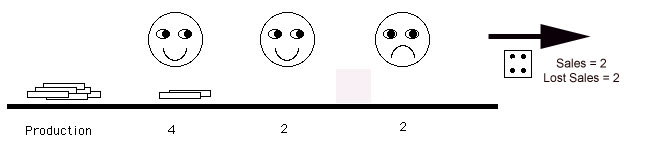
In this first iteration, the system
produces 2 matches. Two matches remain in the system as WIP
waiting for processing by boy 2. This WIP has already been
processed by boy 1 and is available to boy 2 for processing
in the next iteration.
Goldratt told this story to illustrate the negative effects
of statistical variation on a serial production line. The simulation
model allows the system to have as many stations as desired
and the statistical variation to be governed by any of the
common probability distributions. |
The Excel Model |
| |
This story describes a serial
production system with a specified number of stations. To create
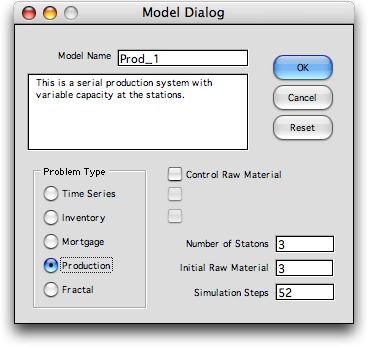
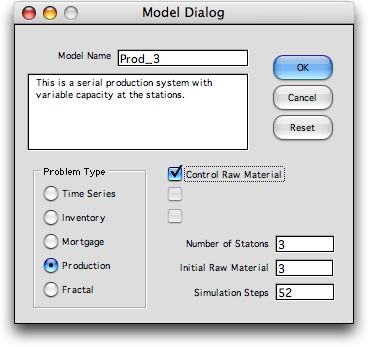
the model in Excel, click the Production button on
the model dialog. The
dialog has a field for Number
of Stations.
The checkbox adds a feature to the model that controls the
flow of raw material into the system. This is illustrated later.
The Raw Material
Supply field
is only relevant if this box is checked.
|
| |
After clicking OK, the multiline
dialog will be presented. Click OK. Then a series of dialogs
will be presented asking about the probability distributions
of the production amount at each stage. The uniform distribution
representing the throw of a single die is the default. The add-in
finally constructs a spreadsheet model of the multistage process.
We illustrate the features below. |
Parameters |
| |
The cost parameters of the model
are below. We assume that an iteration reflects a one-week
interval. The first three entries are the cost parameters.
The inventory cost is the per unit cost of WIP per
week. The cost does not depend on the location of the WIP in
the process. The order
cost is
the cost of placing a nonzero order for raw materials. For
the example, this cost is expended
in every week. It is relevant when manual control of reorders
is controlled manually. The lost sales cost is the
unit cost of demand that is unmet by production.

We have chosen the integer-uniform distribution
for demand and production capacities. The integer-uniform distribution
models the throw of a die. |
Worksheet |
| |
The worksheet illustrates
a three-station example. Station 1 accepts raw material, performs
its operation and then passes the material to station 2. Station
2 performs a second operation and then passes the material
to station 3. After the operation at station 3 the material
enters a finished good inventory. The demanded quantity is
withdrawn from this inventory. If demand is greater than the
amount available, lost sales are experienced. Because it has
so many columns we present the worksheet in two parts.
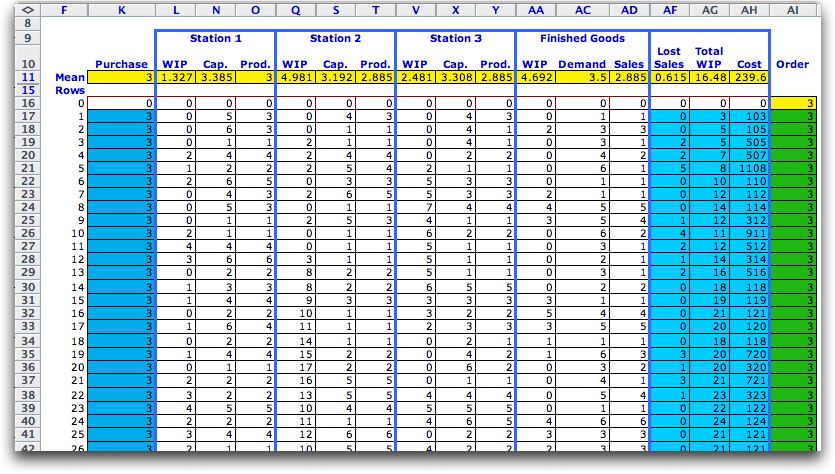
Columns G through J hold the random numbers that
govern the capacities for the three stations and the finished
good demand. Column K holds the materials purchased in each
week. For the example, the purchase amount is exactly the capacity
of the first station. The input capacity is unlimited.
|
|
| |
The station 1 information is outlined
in blue. We review the equations for period 1, row 17 on the
worksheet. Column L holds the input WIP. It is equal to the output
WIP of the previous period. Cell L17 holds a formula that is
"=P16". Since station 1 always produces its capacity, the WIP
is always 0. Column M holds the amount of material available
for production "=K17+L17".
Column N holds the capacity for production. This is a random
amount taken from the RN1 random variable "=RV_sim(Prod_1_Cap1,-G17)".
Column O holds the actual production, "=MIN(M17,N17)".
Column P holds the WIP available for the next period, "=M17-O17".
The results of station 1 are not too interesting, given that
it produces an amount equal to its capacity. Station 2 has more
interesting results. The formulas for station 2 are the same
as for station 1, but the columns references are advanced by
5.
The columns for station 3 and the finished goods inventory
are below. The formulas again are similar to stations 1 and
2. Columns AF compute lost sales, "=MAX(0,AC17-AD17)", total
WIP, "=L17+Q17+V17+AA17", and total cost, "=AG17*Prod_1_Inv_Cost+IF(K17>0,Prod_1_RO_Cost,0)+AF17*Prod_1_LS_Cost". |
|
| |
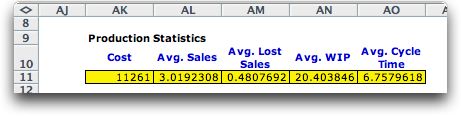
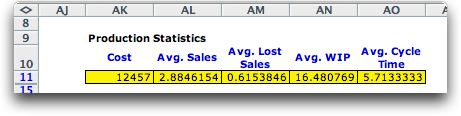
To the right of the station and
demand simulation we see summary results for the 52 weeks simulated.
Although the mean production capacity at each station is 3.5
per week, the average sales per week is just above 3. The average
demand is 3.5 per week, so the lost sales are about 0.5. The
average WIP per week is about 20.4. The average time required
for a match to move from station 1 to sales is the cycle time.
By Little's Law:
Cycle Time = WIP/Sales
For the example the average cycle time is
about 6.8 weeks.
The results indicate that the sequential production
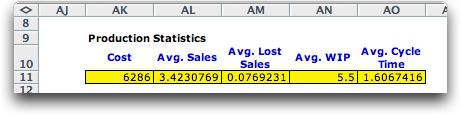
process with statistical variability is not very efficient. The
effect of reducing variability is illustrated when we change
the lower and upper limits on the uniform distributions to 3
and 4. The random variables have the same mean values but much
less variance. The system results shown below are much better.
With integer variables we cannot reduce the variability
to zero and maintain a mean value of 3.5 per week, but we can
set the lower and upper limits to 4. This eliminates variability,
and results in an average production rate of 4. When variability
is eliminated, lost sales, WIP and cycle time all go to zero.
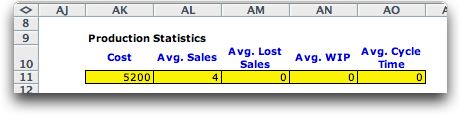
In this model, the minimum cycle time is 0, because
material does not enter inventory if it passes through the system
in a single period. |
Controlling Raw Material Flow |
| |
One suggestion for controlling
a system such as this is to control the input flow of raw material.
This is an option available for the model. To investigate this
option click the Control Raw Material box.
With the control option a new column is included in the model
shown as column AI below. The column shown in green is the
order quantity that will be delivered in the next period. When
the worksheet is created this column has zero's except for
the yellow entry at the top. We have filled in the column with
the value 3. This puts a steady flow of 3 units into the system
at each period. |
 |
| |
The results of the 52-week simulation
are below. Since the average demand is 3.5, there will be lost
sales. Because of statistical variability there is still a
considerable amount of WIP and cycle time is greater than the
minimum value of 0.
|
| |
The control column is very general
in that order quantities can be entered by hand or with formulas.
There are a number of questions one might explore with this model.
- What is the effect of reducing the variability of the production
capacities?
- What is the effect of having more production stations?
The model allows the analysis of any number of stages.
- If one were to add more capacity, would be better at the
beginning of the line or at the end? Capacity is added by
increasing the upper range on the uniform distribution.
- Can a similar simulation be constructed for a pull system
of production, rather than the push system illustrated here?
- Using the control column, how would you model a CONWIP
inventory policy? This policy orders raw materials in exactly
the amounts sold in each period. The WIP remains constant
at the initial value throughout the simulation.
- Would it be useful to adopt an order level-order quantity
policy? In some periods the order quantity could be zero,
thus reducing the reorder cost.
|
The Game |
| |
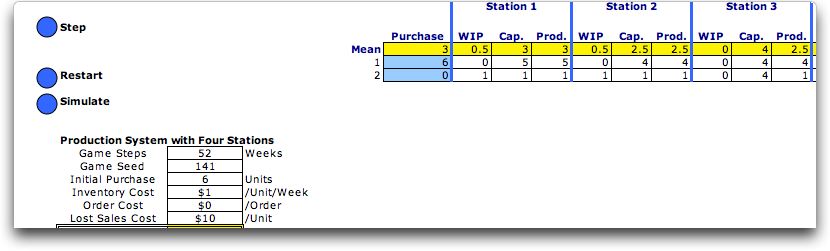
The control option is built into
the Production
Game provided as a template in the Template section
of this site.
The game reveals the situation one week at a time. The student
fills in the order quantity during each period. The goal of the
game is to select order quantities to minimize the total cost
of operating the system. |
 |
| |
|
|



