There is no question that decision making in the face of uncertainty is an important topic.  It is one of the prime activities of man, arising in every field of purposeful work and in most of the games that we invent for our amusement.

The mathematical programming models, such as linear programming, network flow programming and integer programming generally neglect the effects of uncertainty and assume that the results of decisions are predictable and deterministic.  This abstraction of reality allows large and complex decision problems to be modeled and solved using powerful computational methods. 

Stochastic programming explicitly recognizes uncertainty by using random variables for some aspects of the problem. With probability distributions assigned to the random variables, an expression can be written for the expected value of the objective to be optimized. Then a variety of computational methods can be used to maximize or minimize the expected value. This page provides a brief introduction to the modeling process.

Links on this page are to the Stochastic Programming section of the Computation are of this site where the Excel add-ins are used to find solutions to some simple problems in this class. Use the Back button to return to this page.

When we recognize the possibility of uncertainty or risk within the context of mathematical programming, the decision problem might be written as below. The model is shown in the typical matrix format for an LP except tildes appear over all the parameter matrices. This implies that all may be affected by 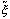a vector of random variables. In practical instances the model could be complicated by nonlinear terms and integrality restrictions. In any event, the model as stated, is not well defined because: (1) the timing of the decisions and observations of the randomness are ambiguous and (2) the concepts of optimal solutions and feasible solutions are unclear.

Stochastic programming addresses the first issue by explicitly defining the sequence of decisions in relation to the realization of the random variables. Given the sequence, an objective function is defined that reflects a rational criterion for evaluating the decisions at the time they must be made. Feasibility conditions must be adapted to the fact that decisions made before the realization of randomness may have feasibility consequences after the realization. How the issues are resolved leads to the several different problems listed below. No single problem formulation is sufficient.

For stochastic programming the probability distribution of 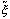must be known. More properly we should say that stochastic programming is decision making under risk, reserving the phrase decision making under uncertainty for those situations for which probability distributions are unavailable. We will, however, use the more popular term, uncertainty, to refer to situations in which distributions are known.

For stochastic programming, some variables are to be set by a decision maker, these are the decision variables, while some model parameters are determined by chance, and these are the random variables. There are a variety of situations one might consider in this context. One differentiation is based on when the decision maker must make decisions relative to the time when the random variables are realized. There are several possibilities. Links on the titles go to pages in the Computation section. The pages open in a separate window.

Wait and See: The decision maker makes no decisions until all random variables are realized.

No Recourse: The decision maker must choose values for the decision variables before any of the random variables are realized. There is a risk of violating the constraints.

Chance Constraints: This is the no-recourse situation when only the RHS vector is random. Solutions are found with specified risks of constraint infeasibility.

Simple Recourse: This topic considers the problem with a random RHS vector. The decision maker must choose values for the decision variables before the RHS values are known, but variables adjusting to the RHS variation are set after the realization. Penalties for constraint violation are specified. A section on Approximations indicates how continuous probability distributions can be approximated for this analysis. An Aircraft Allocation example describes one of the first problems addressed by stochastic programming.

Recourse: Some of the decision variables must be set before the random variables are realized, while others may wait until after they are realized. Models explicitly represent the initial decisions and all recourse decisions. Although the models can be very large, optimum solutions solve for all possible circumstances. A Capacity Expansion example shows that small problems sometimes result in very large models.

Multistage Recourse: Decisions and random variables are determined in stages. The first set of decision variables must be fixed before all realizations. Then the first set of random variables are realized and the second set of decision variables are fixed. The process continues through a series of decisions and realizations. Typically the stages represent intervals of time. We do not consider this situation.

All of the examples on this site describe relatively simple stochastic programming problems, those that we might be able to approach with our Excel add-ins. There is a great deal of high-level research in this field attempting to extend the bounds on the variety of problems that can be practically solved. Most solutions require high-power computation. The reader interested in pursuing this subject further should visit the Stochastic Programming Community Home Page.