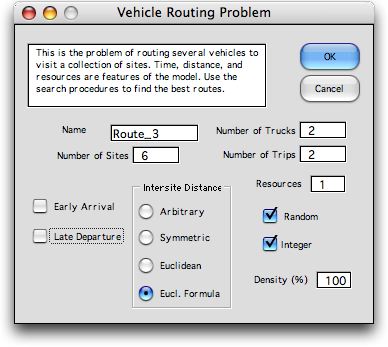
Features of the problem are illustrated by the example. It is the same as used on for the single vehicle problem except here there are two trucks serving the six sites. The two trucks are identified by the headings Depot 1 and Depot 2 in columns D and E of the model. The data in these columns refers to the two trucks. Column L has a third depot entry, Depot 3. This column represents the end of the route.

The distance matrix starts in row 15. A single depot is assumed and the distances related to all depot columns (D, E and L) are the same. We color these entries gray to show that they are determined by formulas and should not be changed directly. The location of the depot in the x, y columns (columns M and N) controls all the distances related to the depot columns.

The initial decisions in row 9 define a route that visits each site in numerical order. Since the first two indices represent separate trucks, the solution does not have interest. It will be changed when we search for the optimum.

One new data item appears below the distance table and that is row 33 holding the resource values. The resource is something that is provided by the truck but is used up by the sites on its route. Resources could represent weight, deliveries, packages or some other measure of capacity. Here we use the site count as capacity and indicate that each truck can visit half of the sites. Each truck has a capacity of 3 and each site reduces this capacity by 1 (the resource contribution of a site is -1). The number labeled P1, the value 1000 in cell M33, is the penalty for violating the resource constraint.

Computations related to the resource are in rows 44 and 45. Row 44 computes the cumulative resource use of the route. Whenever a depot (or truck) is encountered on the route, the resource of the truck is placed in the associated cell. For the example, truck 1 in column D contributes the resource value of 3 in D44. Since the route immediately passes through the depot, truck 2 contributes its resource value of 3 in E44. The resources contributed by trucks do not add as it is assumed that every time the route passes through the depot a new trip begins. As the route proceeds through the sites, the cumulative value of the resource declines until it becomes negative. Columns I though K show negative values in row 44. A negative value indicates a shortage of the resource. Shortages are reported in row 45. The total cost of shortage is the total shortage multiplied by the shortage penalty. It is computed in cell N45. All these quantities are automatically computed with Excel formulas indicated by the yellow color of the cells.

Optimization

We choose a solution method by clicking the Search button on the worksheet. The button calls a dialog from the Optimize add-in for selecting the solution method. The dialog shows the Random search method chosen. This means that 10 random solutions will be generated and the best of the ten solutions will be reported. We did not choose the Exhaustive option in this case because it requires over 5000 solution evaluations.

The results of the random search are shown below. The route follows (Depot 1, 2, 4, 5, Depot 2, 3, 6, 1, Depot 3). This solution implies that truck 1 serves sites 2, 4 and 5, and truck 2 serves sites 3, 6 and 1. Notice that the arrival and departure times indicate that the two trucks operate at the same time, both starting at time 0. The solution has no shortage since each truck serves three sites. The total cost is 555.

To improve the solution, we again click the Search button, but then choose to improve the current solution.

The resultant solution is shown below. The route follows (Depot 1, 6, 5, 4, Depot 2, 3, 2, 1, Depot 3). The total cost of this solution is 513.

The map for this solution is below.

Additional investigation may find better solutions.

With more trips than trucks, a truck may cover more than one trip. The trips occur sequentially in time. To illustrate, consider a problem with a single truck, but with two trips.

The model shows one depot column (column D) at the left of the form, representing a single truck. Two depot columns are at the right (columns K and L). Column K describes the second trip of the truck, while column L is the destination at the end of the route. The resource row (row 33) assigns 3 to each truck and -1 to each site. The solution shown in the figure is the result of the search process described below.

We search for the optimum by first generating 10 random solutions and then improving the best of these. The results are shown below. The route follows (Depot 1, 3, 6, 5, Depot 2, 2, 1, 4, Depot 3). The total cost of this solution is 800. The interesting part of these results is the row labeled Arrive. Although the solution includes two trips, they are both accomplished by a single truck. After leaving site 5 at time 73. The truck arrives at the depot at time 92. One minute later it leaves for the second trip. The truck returns to the depot after the entire route is complete at time 249.

The map describing the solution is below. Notice the first trip indicated by the red lines is much shorter than the second trip. This is due in part to the duration penalty. The penalty causes sites with high site time and located far from the depot to be serviced as late as possible.

The previous examples used multiple trips because of limited resources. Time windows also create the necessity for extra trucks and multiple trips. To illustrate, I created a problem with 20 sites, two trucks and four trips. Each trip is given a resource of 5, so that a feasible solution divides the sites evenly between them. Each site was given a latest departure time of 240 minutes. Although the problem is too large to present here, it is included in the demonstration file for this section. A solution was found by choosing the best of 100 randomly generated solutions. The 2-change improvement method was applied to that solution. A map of the solution is below.

The red and green trips are for the first truck and the black and blue are for the second. The solution shown is not feasible because the first trip has six sites. A feasible solution obviously exists, but the search did not discover one. The solution also has some late departures.