|
|
To model a traveling salesman problem,
choose TSP from the Combinatorics menu.
Our first example has 6 cities. The distances between the
cities are provided by the arc length. In the dialog below
we indicate that the data is to be determined by the Euclidean
measure with the 6 cities located randomly in a plane.
 The initial worksheet is shown below. The solution is
a tour through the cities starting at city 1 and ending
at city 7. City 7 has the same location as city 1 and represents
the completion of the tour. The computer manipulates the
green colored decision variables in row 9 that indicate
the next city in the tour. Row 10 holds the tour and row
11 holds the lengths of the chosen arcs. The sum of the
lengths of the tour arcs is computed in cell F5. This is
the objective to be minimized. Cells H4 and H5 hold the
condition that a tour must visit all cities. The objective
function and constraint cells are all colored yellow to
indicate that they are not to be changed. This add-in only
solves the traditional minimum distance TSP.
The random locations of the cities are shown to the right
of the distance matrix. The cells of the matrix hold formulas
that compute the distances between the locations. The ***
strings indicate disallowed transitions. The initial solution
visits the cities in numerical order. |
|
|
|
The Map button on the left
creates a separate worksheet with a map of the solution. The button
is only available when the x and y ranges in
columns K and L are present. The map of the initial solution is
shown below. The first city is colored gold. |
|
| |
The Search button calls the search dialog from
the Optimize add-in. All the features of this dialog
are described on the TSP page.
For this small problem, we will find the solution by exhaustive
enumeration.
When called from a TSP model created by the Combinatorics
add-in, the search process assumes a linear model, that is,
the arc lengths are computed at the beginning of the process
and used for all subsequent computations. Individual solutions
are not evaluated on the worksheet so the model is less flexible
than models allowed when the TSP model is constructed from the
Optimize add-in. Solution times are therefore much
smaller than when the same problem is solved by Search command
of the Optimize add-in.

The optimum solution is below. The selected cells from the
distance matrix are colored. |
|
| |
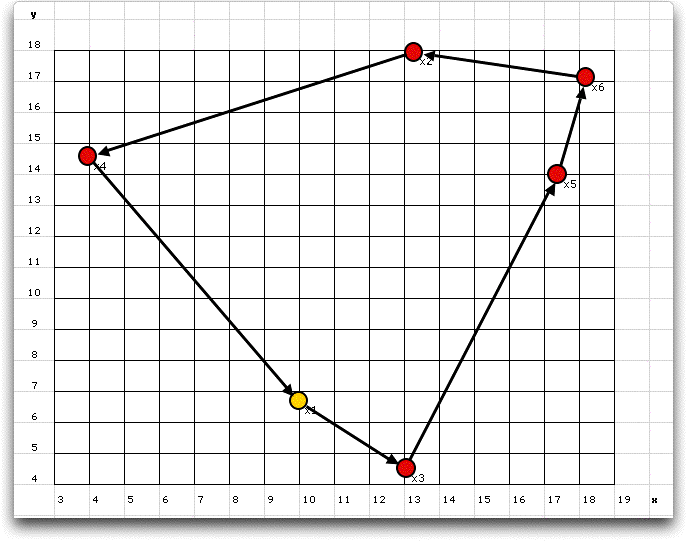
The map of the optimum solution is created by clicking the Map button.
This optimum illustrates the characteristic that the optimum
tour for a Euclidean problem on a plane does not cross. |
| |
 |
48 City Problem |
| |
A well known TSP problem involves the 48 state capitals
in the continental United States. Data for the problem is available
on the web.
The data specifies coordinates for the cities and intercity
distances are computed using the Euclidean measure. We set up
and solved the problem with this add-in. The map of the published
optimum obtained from the web is shown below and has a total
length of 335.237. |
|
| |
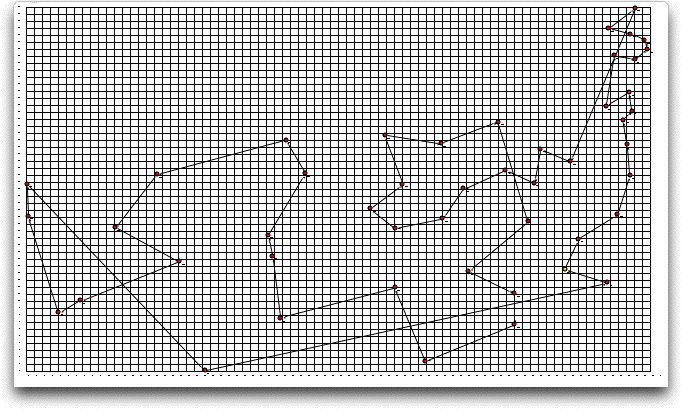
The greedy solution starts from city 1 and the next city is
the one closest to city 1. Subsequent cities are selected to
be the closest non-visited city to the last city added. This
is called the closest neighbor heuristic. The map of the greedy
solution shown below is clearly not optimum. The total length
is 405.264. |
| |
 |
| |
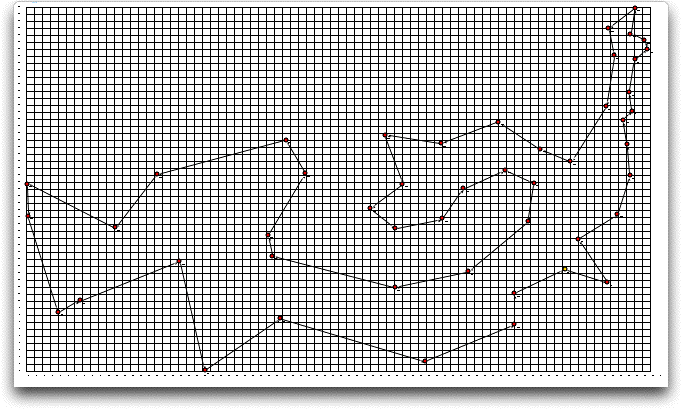
Applying the 2-change improvement procedure to the greedy solution
provides a better solution, but not quite optimum. The total
length is 344.055. The process evaluated 6494 solutions and required
21 seconds on the author's computer. The 2-change procedure first
looks at all pairs of cities (excluding the first and last) and
switches their positions in the sequence. Improving switches
are immediately accepted. This search process continues until
there are no pairs that can improve the solution by switching.
The final solution to this process is followed by the traditional
2-opt procedure. Again we investigate all pairs of cities, but
now when a pair is switched we also change the orientation of
all arcs that fall between them. This tends to change larger
segments of the solution. The 2-opt procedure is repeated until
a pass results in no improvements. The solution tour does not
cross itself. To find a better solution, we might try several
random solutions combined with improvements. |
| |
 |
| |
Solving the TSP problems using the Search button
on the worksheet provides solutions much more rapidly than
solving them using the Search command from the Optimization add-in.
The Combinatorics add-in solves only the traditional
TSP and does not allow additional constraints or a modified
objective function. The add-in makes no assumptions about the
distance matrix and symmetric and asymmetric problems are solved
with the same procedures. This add-in allows the visual display
through maps for Euclidean problems. When distances are provided
by formulas the formulas can be changed to use different distance
norms.
The size of the problem that can be addressed is limited only
by the size of the worksheet, memory limitations and internal
restrictions of Excel. Solution times for larger problems may
become prohibitive and solutions obtained through search procedures
will probably not be optimum. |
| |
|



