|
To model a sequencing problem, choose Sequence from
the Combinatorics menu. We start with a simple case
described by the dialog below. The problem has 6 jobs that must
pass through a single stage of production. No setup time is required
and there are no early or late schedules. These variations are
illustrated later. |
Shortest Processing Rule Example |
| |
|
|
The worksheet is constructed using random data for job
processing times. Two extra jobs are included. A start job
is indexed 1 and an end job is indexed 8. The
six jobs required by the dialog are indexed 2 through 7.
The solution to this problem is a sequence beginning at start and
passing through the six jobs and terminating at end.
The variables defining this sequence are the next jobs listed
in row 9 of the worksheet. The initial sequence performs
the jobs in numeric order.
The solution to this problem is a tour so the
form below identifies the problem type in cell D6 as a
TSP. This cell is used by the Optimize add-in
to control the search process. The other cells in rows
4 through 6 are used by the add-in and generally should
not be changed. Cell F5 holds the formula for the objective
function. Although the proper formula is provided for the
problem at hand, the modeler may change the formula to
represent features not modeled. Cells H4 and H5 hold feasibility
conditions. The formulas provided require that all the
entries in row 9 be greater than 0. Other feasibility conditions
may be added by the modeler. |
|
| |
|
| |
The data items for this example are the process
times, the release times and the duration penalties, entered
in rows 13, 14 and 15 respectively. A job occupies the production
stage for the process time. The release time is the time that
a job is available to begin processing. The duration penalty
is multiplied by the job completion time to determine the objective
value for a solution.
Computed quantities are presented in rows 17 through 26. Rows
17 through 19 and row 21 sort the data according to the current
sequence. When the sequence corresponds to the job indices,
as shown, the data is simply repeated on these lines.
Rows 22 and 23 computes with Excel formulas the start
time and end time of each job for the given sequence.
Row 26 computes the cost for each job by multiplying the completion
time by the duration penalty. For this simple case, all duration
penalties are 1, so all jobs are equally important with respect
to completion time.
The subroutines of the Optimize add-in are used to
find solutions to this combinatorial problem. When all the jobs
have the same duration cost, a greedy solution found by selecting
the shortest job first is the optimum. This is the default greedy
algorithm for the Optimize add-in. To call the appropriate
dialog, click the Search button on the worksheet. The
dialog below is presented. |
| |
|
| |
The results of the greedy process are shown
below. Now the rows starting at row 17 present the job information
sorted in order of the solution. The processing times on row
21 follow the SPT, the shortest processing time, rule.
This is optimum when all duration penalties are 1 and there
are no additional constraints on the solution. |
| |
|
| |
The Chart button creates
a Gantt chart of the solution. Either a vertical or horizontal
presentation is allowed. Since the worksheet has 256 columns
and over 65,000 rows, the vertical presentation is usually preferred.
A column or row is required for each time interval. The total
time for the example is too long to display on this page, but
we show below the Gantt chart for an smaller example. The chart
is created on a separate page from the data. The start and the
end cell are colored white. The job cells are colored based
on the index of the job. In order for a job to appear, it must
have a processing time of at least 1. We have specified the
processing times of the start and end as 1 so that they appear
on the chart. |
| |
 |
Example with Stages |
| |
It may be that a job may be required to pass through several
stages of a production process. A system of this type is a flow
shop since we are assuming that every job passes through
all the stages, and the sequence of jobs at each stage is the
same. To illustrate stages and setup times we create
a second example.

The data for the example is shown below. The solution
is obtained with exhaustive enumeration, only possible because
the problem has only six jobs. |
| |
|
| |
The computed results for the optimum solution
are below. The finish time for the jobs are the end times for
stage 3 of the system. There are two restrictions on when a job
may begin at some stage. The job cannot begin on a stage until
the setup and processing times for all previous jobs on that
stage are complete. Also a job cannot begin on a stage until
the job is finished on the previous stage. At stage 1, a job
cannot begin until its release time. When both the restrictions
are satisfied, the job begins. |
| |
|
| |
|
The effects of setup times
are illustrated by the partial Gantt chart at the left.
The first job (after start) is job 6 with a setup
time of 1 and a processing time of 6. Setup times are in
black and job 6 has the brown color in the Gantt chart.
Although stage 1 processing is complete and job 6 is available
for stage 2 at time 7, it cannot begin processing at stage
2 because of the setup time of 9 periods for job 6 at stage
2. Note that we are assuming that a job can be setup for
the next stage during an idle time before the job actually
is available. After completion of stage 2, job 6 can immediately
begin on stage 3. The setup time for job 6 on stage 3 is
performed before job 6 arrives. There are some time intervals
near the bottom of the figure with no color. During these
periods the stages are idle. For example stage 3 is idle
for one period from time 41 to 42. Job 3 does not arrive
until time 46 and the 4 periods of setup time need not
begin until time 42. In general, stage 1 will remain entirely
occupied until all jobs are complete in stage 1. Later
stages may have idle times.
The exhaustive enumeration procedure generates and evaluates
all feasible solutions. The best 19 of these are shown
below. The optimum solution is evaluated twice.

|
|
Early Start and Late Finish |
| |
We use the same data as the last example, but
allow scheduled start and finish times by clicking the check
boxes.
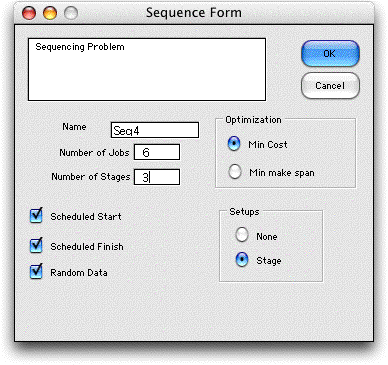
The data for the example is below. Rows 9 and
10 hold the optimum solution. The default value for the scheduled
start is 0 and the default value for scheduled finish is a
large number, so the default values do not affect the solution.
We have specified a scheduled finish of 100 for job 1 and a
schedule start and finish for job 3 of 110 and 150. In addition
we provide a nonzero release time of 50 for job 6. All these
restrictions are violated for the optimum solution obtained
in the last section except the scheduled finish for job 3. |
| |
|
| |
The results are shown in the arrays starting
at low 28. Row 28 has the optimum sequence job titles and row
29 holds the associated indices. The release times, process
times and setup times are repeated but sorted according to
the solution. The start and end times for the three stages
are computed.
From the solution we see that job 6 begins processing in stage
1 at time 50, exactly its specified release time. Release times
are hard restrictions in that a job cannot be started on the
first stage until it is released. Job 3 has a scheduled start
time of 110. We see from the results that the start time for
job 2 is 112. The program penalizes start times that are before
the scheduled start but does not penalize start times after
the scheduled start. Row 47 shows a positive value if a job
is started early, the difference between the scheduled start
and the actual start in stage 1. Note that setup for the job
may take place before the job is actually started.
Finish times will be penalized if they occur after a scheduled
finish. For the example we see that job 3 is finished (end for
stage 3) at time 152. The scheduled finish is 150, so the job
is late by 2 periods. The lateness is computed in row 48. The
finish time for job 1 is 84, well below the scheduled finish
of 100, so this job is not late.
Rows 50, 51 and 52 hold the costs computed for duration, early
start and late finish. The objective function value is the
sum of the yellow colored cells of these rows. |
| |
|
| |
The combination of early scheduled start and
late scheduled finish is usually called a time window for sequencing
problems. This example treats time windows as soft constraints.
Early starts and late finishes are penalized but not prohibited.
The results shown here were determined by exhaustive enumeration.
The same solution was obtained for 10 random searches, each
followed by the 2-change procedure. Some combination of heuristic
methods will be necessary for larger problems. The number of
columns on a worksheet limit problems to about 120 jobs. Even
heuristic methods will have trouble with this size problem,
because every solution tested requires an evaluation of the
worksheet. |
| |
|



