| On this page we use
a different add-in to solve the layout problem.
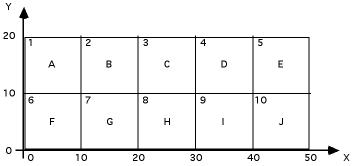
Some layout problems can be modeled as
quadratic assignment problems. An example is shown in the figure
below. Here we have 10 offices indicated as A though J and they
are all the the same size (10x10). There are 10 possible locations
for the departments, indexed 1 through 10, with the same dimensions
as the offices. The figure shows the departments assigned in
numerical order.
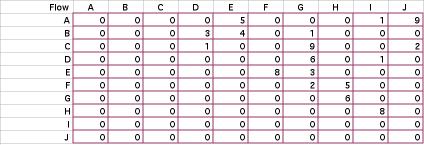
The flow between each office is shown
in the from-to matrix below. We only show flow in one direction,
but since the distances between departments are symmetric, it
is unnecessary to specify direction.
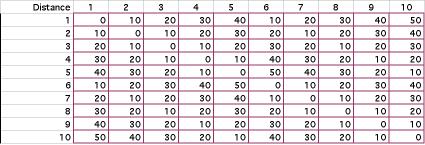
We assume that the length of individual
trips between the departments is measured by the rectilinear
distance measure and that travel is between the centroids of
the departments. The distance between the centroids of the 10
locations is computed in the matrix below.
The problem is to assign locations to
the offices to minimize the flow-distance measure. To evaluate
the natural assignment shown in the example we multiply each
number in the distance matrix by the corresponding number in
the flow matrix and add the numbers. The result for the initial
layout is 2100.
The problem described is an example of
a quadratic assignment problem (QAP). This problem is addressed
by the Combinatorics
add-in. The Optimize
add-in is used for the analysis, so it also must be installed.
For a discussion of the use of QAP for layout problems
go to the QAP
page of the Combinatorics add-in. The assignment
determined by the add-in is shown below. The value of this solution
is 950. |



