Several problems are solved by finding an optimum permutation of the first n integers. As an example consider the simple assignment problem. There are n tasks and n machines. A cost is specified for completing each task with each machine. The problem is to assign one task to each machine so that all tasks are completed with the smallest total cost. This is a combinatorial problem whose solution is described by a permutation of n integers. For a seven task problem one solution is given by the permutation: (1, 2, 3, 4, 5, 6, 7). This implies assigning task 1 to machine 1, task 2 to machine 2 and so on. Every permutation describes an assignment.

The linear assignment problem just described is one of the simplest of the combinatorial problems and can be solved with linear programming as well as with several special purpose algorithms. Here we formulate and solve the problem as a combinatorial search problem. Although this is a poor choice from a computational point of view, it serves to illustrate the features of the Optimize add-in for permutation problems. There are a number of problems whose solution is a permutation that that are not so easy to solve including the quadratic assignment problem and the facility location problem. These problems are solved in the Combinatorial add-in and the Layout add-in with procedures that call the permutation option of this Optimize add-in.

To create a permutation model choose Add Form from the Optimize menu. In the dialog click the Permutation button and enter the number of variables into the appropriate field.

With the data table box checked a square matrix is included to hold the cost of the assignments. With the data table, the problem definition is complete and the model may be solved directly. Without the data table, the user must construct the formulas for the objective function and feasibility conditions.

The add-in places the permutation form on the worksheet with the upper-left corner located at the cell specified in the dialog. The data for a 7 task-machine assignment problem is shown below in the range labeled Obj. Coef. The table shown holds randomly generated data. Row 0 is used by the program and should not be changed. We arbitrarily call the rows tasks and the columns machines.

The decisions in row 7 are a permutation that represents an assignment. The initial solution assigns task 1 to machine 1, task 2 to machine 2 and so on. The program uses the Excel Index function in row 9 to return the cost for each machine, and the total cost is computed in cell D3.

Note that this combinatorial representation of the assignment problem is much different than the representation used for linear programming models. For the latter, the variables take on the values 0 and 1 where x(i,j) = 1 if task i is assigned to machine j and 0 otherwise. The LP model has a constraint for each task and each machine that assures that every task is performed exactly once and every machine is used exactly once. In the combinatorial model the values are integers that range from 1 to the number of tasks. The objective function is not linear since it uses the Excel Index function. This model is concise with only 7 variables and no constraints while the linear programming model has 49 variables and 14 constraints (one is redundant).

In the present case one pays for the combinatorial simplicity with computational tractability. While the LP model is easy to solve, the combinatorial model requires an exponential optimization procedure or approximate solutions.

Solving the combinatorial model by exhaustive enumeration requires that 5041 permutations be evaluated. Only permutations are generated and each is placed in row 7 of the combinatorial form. The worksheet functions compute the value of each solution and the add-in keeps track of the best 20 found. The results for the example are below.

This method can be adapted to a variety of permutation problems other than the assignment problem by changing the formulas that compute the objective function. Whatever the objective, the results must be a function of the permutation and be computed in cell D3. Although we have not used the Feasibility cells (F2 and F3) for the assignment, these cells might be useful for other problems that have feasibility conditions not otherwise modeled.

Random Search

Of course, exhaustive enumeration is possible only for small dimensions. The add-in provides heuristic methods to search for the optimal solution for larger problems. One method is to generate permutations at random. By clicking the Improvement button on the Search dialog, each randomly generated solution will be subjected to the improvement procedure.

Greedy Solution

Another option is to use a greedy approach to find a solution. This is a constructive procedure that adds one machine-task assignment at a time. When a data table is present, the program computes the difference between the smallest number in a column and the next smallest number. The first assignment is made in the column with the greatest difference. The row with the smallest cost is chosen for the assignment. 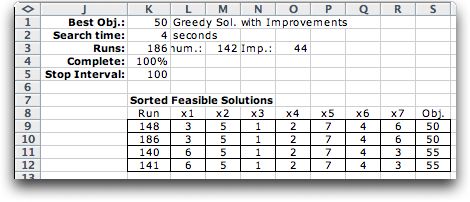Subsequent assignments compute column differences and make assignments from rows and columns that have not already been used. The table below shows the results of the greedy assignment followed by an improvement step. The greedy solution is obtained in run 140. The improved solution was obtained in run 148 by switching the assignments for x1 and x7. The improved result is not the optimum.

The greedy approach takes a number of objective evaluations that involve incomplete assignments. The greedy approach only finds a feasible solution at the last step.

When the data table is not present, the objective computation must be provided by the user. Every observation requires an evaluation of the worksheet and the greedy approach may take quite a few evaluations, but the effort generally takes a small time compared to the other search approaches.

The greedy approach often encounters tie values during the construction process. When this occurs the assignment pair is chosen at random. When ties are present, several calls for greedy search may yield different solutions. A box on the search dialog allows the program to perform several greedy searches sequentially.

Improvement

Given a permutation, the values for any set of variables may be switched and the result will still be a permutation. The program uses an n-change switching approach in the search for improvements, where n-change is at least 2. With n-change equal to 2, all pairs of variables are considered and the values of the variables are temporarily switched. The resulting permutation is evaluated and if the objective value is improved the two values are switched for the subsequent steps of the process.

The add-in allows larger values of n-change. With a value of 3 all interchanges of three variables are considered. As n-change becomes larger the number of improvement evaluations increases considerably but the final result may be closer to optimum. A value of n-change equal to one fewer than the number of tasks is equivalent to exhaustive enumeration.

For n-change greater than 2, the process starts by investigating all possible 2-variable switches. The process continues until a complete pass through the entire set results in no improvement. Then the process considers all 3-variable switches until no improvement is observed. The process continues to consider changes until the specified n-change value is reached. For any number of switches we require that all switched positions be changed. This assures that k-variable switches do not repeat switches already considered with fewer than k variables.

The improvement process can be applied to the current solution on the worksheet, the results of the greedy procedure, or to each of a set number of randomly generated solutions. The latter case is often a good heuristic since it combines the impact of random generation and improvement. Only a few random solutions should be generated with this option because the number of random solutions multiplies the number of improvement evaluations.