|
|
 |
Process
Flow Models |
 |
- Defects
|
 |
A principal
cause of waste in a production process is the introduction of
defects. The possibility of defects leads to the necessity of
inspection. The results of inspection may be the discard of the
product as scrap or routing to a rework facility. The discovery
and repair or discard of defective items results in additional
variability in the production process. There is also the possibility
that a product with an undiscovered defect is shipped to the
customer. When the customer ultimately discovers the defect there
is the cost of warrantee repair and the loss of customer good
will. All these results are waste. This section describes the
mathematical models used by the add-in to model the creation,
combination and discard of defective items. |
| |
|
The defect feature
of the model is added by checking the Defect checkbox.
The figure shows that the Proportion box is also
checked as the defect model requires the proportion feature. |
Figure 1
|
A number of kinds of defects might be introduced by
a production process. A fatal defect when present in
a product will cause the product to fail in some way
to satisfy its specifications. In this section, we restrict
attention to fatal defects.
For analysis purposes, we define the probability that
operation i introduces a defect into a unit of
product as  .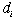
To compute the defect probability associated with two or
more operations, we assume that the events producing defects
are statistically independent.
Fatal defects are discovered only through inspection.
If discovered, a defective item will be discarded as scrap.
If not discovered, a product with a defect will pass to
other operations to receive subsequent processing. If the
finished product leaves the process with a defect, it is
ultimately discovered by the final inspector, the customer.
Although an item may be made defective by more than one
operation, one fatal defect is sufficient to cause the
failure of the product.
No defects are discovered at non-inspection operations,
however, there may be other sources of scrap at these operations.
For example, a non-inspection operation may have a scrap
factor that represents material removed and discarded.
We also may identify a second kind of fatal defect that
can be immediately observed by the operator and discarded.
For instance the operation may break the item causing immediate
discard. Both these mechanisms will be incorporated into
the scrap proportion for the non-inspection operation.
We assume that discards of this fashion do not affect the
defect probabilities or the way in which the probabilities
combine to determine the removal rate at inspection operations.
To illustrate, consider the process with four serial operations
followed by an inspection station as in Fig. 1. Assume
that each operation introduces fatal defects in 10% of
the items passing through it. The inspection station is
perfect in that it finds and removes all defective items.
The inspection operation is shown as a rectangle in the
figure. The process worksheet with this data is shown below
along with the computed results. Note that an inspection
station is identified by the word "Inspect"
in the Type column. Only the first two letters are used,
so alternatives such as "In" or "Inspect
1"
also represent inspections.
The Defects Out column shows the proportion of
the items that are defective at each operation, and the Flow
Removed column shows the proportion that are removed
from the flow. Note that the defects accumulate in the
flow as it passes through the process. When items finally
reach the inspection station, the defects are discovered
and approximately 35% of the flow is discarded. Since this
example assumes perfect inspection, the defect rate at
the output of the inspection is zero. The effect of the
discard of so many defects is to increase the unit flow
to over 1.5 for all the operations. For each unit that
passes out of the process, 1.5 units must be processed.
The throughput time and WIP is increased proportionally. |
|
|
| |
The
following describes the columns that are important for the
discussion of defects. |
| |
Data Items and Result Items for the Example
Column |
Title |
Explanation |
G |
Defect Rate |
This is the percentage of products
passing through a processing operation that receive defects.
We assume a single defect warrants discard of an item,
however, the defects are only discovered by an inspection.
Defects do not change the flow except for an inspection
operation. For an inspection operation, the defect rate
is the proportion of defects not discovered and
discarded.
|
H |
Proportion |
For a pull system, this is
the proportion of the flow entering the next node that
comes from the operation specified by this data line. For
a push system, this parameter is the proportion
of the flow leaving the operation that goes to the next
operation. The proportion column is necessary when defects
are present.
|
M |
Defects
Out |
For a processing operation ("Op"),
this is the proportion of the items leaving an operation
that have defects. We assume that the defect producing
mechanisms in different operations are independent. The
function in this cell combines the probabilities of defective
parts entering the operation with the defect probability
for the operation to obtain the probability that an item
leaving the operation is defective.
For an inspection operation ("In"), the probability
of a defective part leaving is zero if the inspection
is perfect, that is inspections find and remove all defective
items. If the inspection is not perfect, the function
computes the probability that a defective item leaves
the inspection.
|
N |
Flow
Removed |
For a processing operation, this
cell then contains the adjusted scrap rate for the operation.
When the operation is an inspection, defective items are
removed as waste. The proportion discarded is shown in
this column.
|
O |
Ratio |
This is the ratio between output
flow and input flow for an operation.
|
|
Pull
serial process |
| |
Fig. 1 is an example of a pull serial process.
The flow is not affected by defects until it reaches an inspection.
There, some or all the defective items are removed. To compute
the amount removed, we must first compute the probability
that an item entering an inspection is defective. When inspection
is perfect, this probability becomes the removal rate at the
inspection operation.
Consider the example in Fig. 1. Assuming the
material entering operation 1 has no defects, the probability
that a defect is produced is  .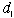
Since they are not removed, defective units are still processed
in operation 2 along with the non-defective ones. Assuming
independence, we can compute the following probabilities about
the output of operation 2.
These probabilities are computed in the Defects
Out column, where we see 0.1 as the probability of a
defect at the output of operation 1 and 0.19 at the output
of operation 2. There is a 0.01 probability that an item has
two defects after passing through the first two operations.
The remaining entries in the Defects Out
column are computed similarly using a recursive relation
The Flow Removed column (J) shows the
proportion of the flow that is discarded as scrap. For non-inspection
operations, no flow is removed. For a perfect inspection,
the scrap rate of the inspection operation is set equal to
the defect probability at its input and the proportion of
defects out becomes 0. When the inspection is not perfect,
we use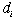
as the probability that the inspection does not detect a defect.
|
Push
serial process |
| |
Figure 2
|
The effect of defects in a push serial system are
the same as for the pull serial system as illustrated
in Fig. 2 and in the worksheet for this process. The
defect rates are the same as for the pull example,
but the flows are different because of the different
drive mechanism for the push process. For every unit
entering node 1 approximately 0.66 units leave node
5.
|
|
|
Pull
non-serial process |
| |
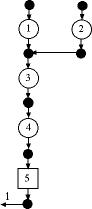
Figure 3
|
We observe the effects of defects in a non-serial
process in Fig. 3. When two or more branches come together,
as the outputs of 1 and 2, the probabilities of defects
combine.
Thus we have at the output of operation
3, the probability of defect:
1 - (1 - 0.1)(1 - 0.1)(1 - 0.1) = 0.271
The results for the example in Fig. 3
are almost the same as the results for the example
of Fig. 1. The only difference is for operation 2 that
has a defect probability of 0.1 rather than 0.19. This
does not affect on the unit flows, because the same
number of defects are produced and are not eliminated
until the inspection station is reached at the end
of the process.
|
|
|
| |
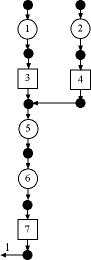
Figure 4
|
The process of Fig. 4 is the same Fig. 3 except we
add inspection stations before the assembly operation
at 5. The operations have been renumbered to meet the
restrictions of a tree structure.
The Excel worksheet for the example shows that the
extra inspection stations reduce the unit flows in
all the operations. The throughput time and WIP are
increased because of the extra inspection time.
For a process with defects, the problem of finding
the optimum location and number of inspection stations
is relevant. With additional cost information, this
add-in can guide the search for an optimum.
|
|
|
Push/tree
structures |
| |
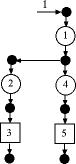
Figure 5
|
The process of Fig. 5 is a push tree. Defects are
produced in operations 1, 2 and 4, and removed at the
inspections at 3 and 5.
The analysis of a push tree is easier
than for a pull tree, since each operation in a push
tree has at most one predecessor. To illustrate, consider
operation 1 in the figure. Assuming the material entering
operation 1 has no defects, the probability that a
defect is produced is .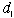
Although defective units may be produced in operation
1, they are still processed in operations 2 and 4.
Assuming independence, we can compute the following
probabilities about the output of operation 2.
These probabilities are computed in the Defects
Out column. We see 0.1 as the probability of
a defect at the output of operation 1 and 0.19 at
the output of operation 2. There is a 0.01 probability
that an item has two defects after passing through
the first two operations.
The same computations can be made for
operation 4 which also receives its input from operation
1. Since all have the same defect probabilities, we
find the probability of defect at the output of 4 to
be 0.19.
The remaining entries in the Defects
Out column are computed similarly using the
recursive relation
The Flow Removed column (J)
shows the proportion of the flow that is discarded
due to defects. For non-inspection operations, no flow
is removed. For a perfect inspection, the removal rate
at the inspection operation is set equal to the defect
probability at its input and the proportion of defects
out becomes 0. When the inspection is not perfect we
use 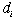as
the probability that the inspection does not detect
a defect.
|
|
|
Network
Structures |
| |
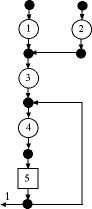
Figure 6
|
The formulas for defect probabilities are applied
recursively, starting at the operations with the lowest
indices and passing to operations with higher indices.
The indexing for the operations of a tree assures that
this recursive approach is successful. For the more
general network structures, the recursive process is
not valid.
The add-in does not disable the defect option for
network structures, but it should be used with caution.
An example is in Fig. 6. This network structure is
the same as Fig. 3, but part of the output of inspection
station 5 is routed back to operation 3 for additional
processing. We assume that 80% of the input to operation
4 comes from operation 3, while 20% comes from operation
5.
Not considering the branch from 5 to the input of
4, the structure is a tree. We model the defects using
only that tree. In fact, this is valid for this example,
because the items routed from operation 5 do not contain
defects. The Excel model is below. The Next and Proportion columns
describe the tree structure and the Transfer In matrix
defines the network structure. It is important that
the two models are consistent.
|
|
|
Proportions |
| |
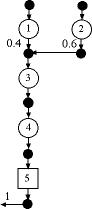
Figure 7
|
Most of the examples to this point used branch proportions
of 1. Here we consider situations in which proportions
may be other than 1. For pull/tree structures it is
necessary to adjust the defect formulas. Consider the
situation of Fig. 7. The numbers on the branches entering
operation 3 imply that 40% of the items passing through
operation 3 receive items from operation 1 and 60%
receive inputs from operation 2. To compute the defect
probability for an operation receiving several inputs
we use the following general expression.
For the example, we have at the output
of operation 3, the probability of defect:
1 - (1 - 0.1)[1 - (0.4)(0.1)][1 - (0.6)(0.1)]
= 0.1878
This result is rounded to 18.8% on the
worksheet below.
For the push tree the defect probabilities
are not affected by branch proportions.
|
|
|
Grouping
Factors |
| |
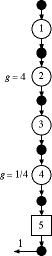
Figure 8
|
In the example of Fig. 8, four items from operation
1 are grouped to form a single item passing out of
operation 2. For example, four sheets of plywood might
be glued at operation 2 and four individual sheets
becomes one assembled item for subsequent processing.
At operation 4, the process divides the item in some
manner, so that one item becomes four in subsequent
processing. Continuing with the plywood example, perhaps
operation 4 cuts the assembled plywood sheets into
four individual smaller parts.
Grouping factors are useful in a variety of contexts
and defect probabilities must be adjusted to account
for them.
The expression assumes that the items
are grouped prior to the operation. Any defects produced
at the operation are not raised to the power.
In the example, we introduce 10% defects
in operation 1 with no further defects in the subsequent
operations. At operation 2 we group four of the items
into one. The defect probabilities for the operations
are computed recursively, starting from operation 1.
|
|
|
User
Defined Functions |
|
|
The defect proportions are computed using User Defined
functions provided by the add-in. There are two different
functions used in pull and push trees respectively. The function
used for pull trees is:
= pull_defect(op_type, index, next_range,
prop_range, defect_range, d, g)
The arguments labeled range refer to
the named ranges on the Excel process definition. Algebraically
the function computed is:
For push trees the appropriate function is:
= push_defect(op_type, prev, index_range,
prop_range, defect_range, d, g)
The arguments labeled range refer to
the named ranges on the Excel process definition. Algebraically
the function computed is:
The functions are placed in the Defects
Out column. The arguments on the worksheet are references
to the cells holding the appropriate parameters.
The process definition also uses functions to compute the
amount removed at the operation. These functions combine the
effects of scrap removed at an operation and items removed
due to defects. Different functions are required for pull
and push trees.
= pull_remove(op_type, Index, next_range,
prop_range, defect_range, Scrap, d, g)
= push_remove(op_type, prev, index_range,
prop_range, defect_range, Scrap, d, g)
The functions are placed in the Flow Removed
column of the process definition. The contents of the Flow
Removed column is used to compute the Ratio column.
|
| |
|
|
