|
|
 |
Process
Flow Models |
 |
-
Production Lines
|
| |
When portions
of the process are arranged into time-paced production lines,
the operation time does not entirely determine the amount of
resource time used by the operations in the line. A line is
characterized by it's cycle time, the time interval between
the departure time of units leaving the line. The operations
in a line are paced to this cycle time. When the operation
time is less than the cycle time, the resource performing the
operation remains idle for a time equal to the difference between
cycle time and operation time.
A line can accommodate operations with times greater than
the cycle time by providing parallel stations. For example,
if an operation time is 9 minutes and the cycle time is 5 minutes,
two parallel stations must be required. Each station requires
two line cycles for a unit of product.
For this case we use the time_f (time function) to
compute the extra resource time required for an operation that
is part of a production line. |
| |
|
As illustrated previously, we
must choose the Time Function feature when
building the process definition.
To illustrate the use of the time
function feature, we use the example previously to show
defects, but here we assume that the processing operations
and inspection operation are arranged in a paced line.
Although the operations have different processing times,
the line is operated so that every unit of product remains
at each station for the same amount of time.
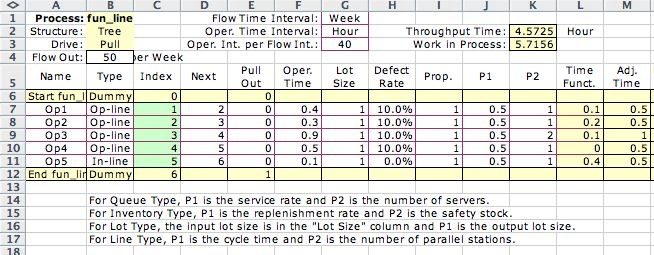
The line function is invoked by
including the word "line" as part of the Type definition
in column B below. The time function is computed in column
L. For a line operation, the function depends on the
cycle time of the line included as the P1 entry in column
J. It also depends on the number of parallel stations
provided for the operation placed in column K. For an
operation in a line with a time longer than the cycle
time, more than one station must be provided. Multiple
stations process units simultaneously. The delay in time
caused by the line operation is computed with the formula
below and presented in column L.
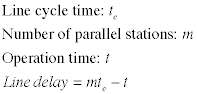
|
|
| |
|
 |
For the example, we use a cycle time of 0.5
hours. Because operation 3 has a processing time of 0.9 hours
we use two parallel stations for this operation. When a unit
passes through this operation, two cycles of the line must
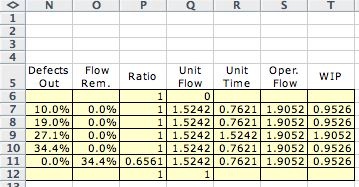
pass (1 hour) before the unit is released. The function computed
in column L shows that 0.1 hour of resource time is lost.
For operations with only one station, the lost time is simply
the difference between the operation time and the cycle time.
With a demand for 50 units per week, the operation
flow is 1.9052 per hour. The WIP indicated in column T indicates
that the line has sufficient capacity to carry this load.
|
| |
|
|



