|
|
 |
Process
Flow Models |
 |
- Downtime
|
 |
There will be times
when a process experiences downtime, that is, time when the
resources associated with production becomes idle. Downtime
may be caused by a failure of a machine that causes production
to stop until the problem is located and repaired. It may also
result if some raw material is unavailable. Then production
must stop until the raw material is obtained. Usually, downtime
is disruptive and should be eliminated if possible, but a correct
model should recognize the existence of downtime.
We accommodate downtime by providing a column on the data
form. A number entered in the column for a particular operation
represents the expected downtime per unit produced. The time
is accumulated in the Adjusted Time column and ultimately
is included in the Unit Time. Downtime expends the
time available on a resource and thus reduces the time available
for useful production.
There are mechanisms that cause an entire process to go down.
Such times should be included for all operations in the process
affected. All downtimes must be expressed as expected times
per unit of production. |
| |
|
To include downtime
in the analysis, click the Downtime button on
the dialog. To keep the example simple, we do not select
the remaining options.
The example has five operations arranged in series.
The demand for the product is 40 per week and the operating
interval is 40 hours per week. With no losses, this results
in a flow rate of 1 per hour as shown in column M. The
operating times are shown in column F. If each operation
were implemented in a separate station, the WIP in column
N shows that all the stations average 1 or less product,
so one station for each operation is sufficient when
all downtimes are equal to 0. |
|
| |
|
 |
For purposes of illustration, assume that 1%
of the items passing through the line will cause an event
that results in the entire line being shut down. Further
assume that the average downtime caused by this event is
2 hours.
With a flow of 40 per week, the expected downtime for the
system is 40*0.01*2 = 0.8 hours per week. Expressed as a
per unit amount this is 0.8/40 = 0.02 hour per unit.
A second event that occurs at a rate of 1%
of the units process, causes only operation 4 to shut down.
This downtime is 10 hours for each event. By the same reasoning
this adds an additional 0.01*10 = 0.1 hours per unit at operation
5.
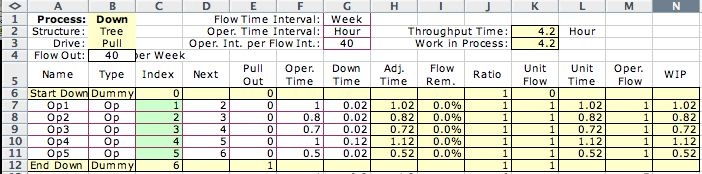
The resulting downtimes are added on the form below.
|
| |
 |
| |
The WIP values now indicate that a single station is no longer
sufficient for operations 1 and 4 since the values
are greater than 1 for these operations.
Not shown by this analysis is the disruptive effect of the
randomness of the downtime events. When the entire process
shuts down, the materials in process remain at the idle production
stations, so when the process restarts there is no marked
redistribution of WIP. When a single station is affected
and the other stations
continue processing, problems of supply arise when stations
downstream of the downed station become starved and inventory
piles up at the downed station. This analysis does not show
this effect.
When disruptive events concerning a single station are allowed,
inventory must be maintained to buffer the effects of downtime.
The add-in does provide an inventory option through the Time
Function feature, but the parameters of the inventory
must be externally set.
|
| |
|
|



