| |
 |
We consider again
an independent inventory with finite replenishment rate. In
this section we allow shortages. That is, we allow the inventory
to run out and customers who arrive and find the inventory empty
do not receive immediate satisfaction. The unsatisfied customers
will respond in one of four ways.
- The customer will wait for delivery until the next replenishment
but there is a cost associated with waiting that is proportional
to the waiting time. This is called the backorder case.
- There is a fixed charge that occurs whenever the event of
shortage occurs during a cycle. The charge is independent
of the number of shortages that occur.
- The customer will wait for delivery until the next replenishment
but there is a cost associated with dissatisfaction that is
a constant, independent of the waiting time. This is called
the fixed shortage cost case.
- The customer will not accept delivery at any future time
and the sale is lost. This is called the lost sales case.
The first three cases involve backordered shortages, while
the last involves lost sales. We consider the backorder cases
on this page.
The finite model is often used when the inventory is being
replenished by a production process. The backorder case is not
realistic when the material being drawn from the inventory is
another production process. A process cannot wait for backordered
items. The model only has relevance when customers can wait
for delivery. |
Finite Replenishment Rate with Shortages Backordered |
| |
This situation is
similar to the infinite replenishment case except that inventory
is replenished at a finite rate P which is greater
than the demand rate D. As shown in the figure below,
the inventory position does not reach the extremes of the infinite
case.
|
Formulas for Instance Results |
| |


Click buttons to see the notation
|
Here
we derive the formulas for the results for an instance.
In addition to the inventory parameters, two variables
are necessary to describe the pattern in the figure. As
for the finite replenishment case, we use the variables
lot size, q and fill rate, v. The fill
rate is the proportion of the demand that is satisfied
immediately from inventory. The proportion that is not
satisfied from inventory, but is backordered is 1-v.
This model assumes that the cost of a backordered item
is proportional to the waiting time. The backorder cost
per unit time is 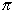 .
Click the Parameters button on the left to see
the definitions of the parameters and variables used for
the analysis. We will derive formulas for the quantities
defined on the page reached by the Results button.
These formulas are implemented in the Inventory add-in. .
Click the Parameters button on the left to see
the definitions of the parameters and variables used for
the analysis. We will derive formulas for the quantities
defined on the page reached by the Results button.
These formulas are implemented in the Inventory add-in. |
|
| |
To construct the
model describing the costs or profits associated with the inventory
system, we show the cash flows below. The blue area indicates
revenues from sales from the inventory. The revenue has two
components. The rate of revenue is RP during the interval
when the shortage is being satisfied and RD after
the shortage is satisfied and demand is drawing the inventory
down. When the on-hand inventory reaches 0, there is no revenue.
The expenditure for product cost is CP during production.
The red area represents holding cost and the purple area represents
backorder cost. The fixed setup cost A is incurred
at the beginning of each cycle.
|
| |
A single inventory cycle is shown
below.
|
| |
The table below shows the various
revenue and cost components and their respective cost rates.
We compute the holding and backorder costs during a cycle with
expressions for the associated triangular areas. The rates
are the cycle costs or revenues divided by the cycle time.
Item |
Amount during a cycle |
Cost or revenue rate |
|
A |
|
Product Cost |
Cq |
|
Holding Cost |
|
|
Backorder Cost |
|
|
Revenue from product Sales |
Rq |
RD |
|
| |
For this model there are two decision
variables q and v.
|
| |
Additional quantities associated
with the inventory policy are derived below.
|
| |
All realization results are the
same as those computed for the infinite replenishment case
except they are multiplied by the factor (P - D)/P.
This factor goes to 1 as the production rate increases without
bound.
The measures are computed below for the example using a lot
size of 400 units and a fill rate of 90%. The figure shows
a single cycle of the inventory pattern.
|
Optimum Policy |
| |
For determination
of the optimum lot size q* and fill rate v*,
the unit revenue and unit purchase cost can be neglected and
we write the expression for the cost rate for operating the
inventory.
We first take the partial derivative
with respect to the fill rate.
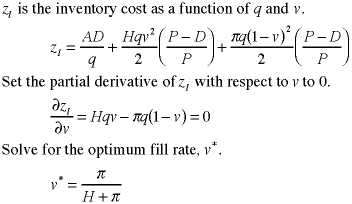
The optimal fill rate is is the same as
for the infinite replenishment rate case.
We next take the partial derivative with
respect to the lot size.

The optimum lot size is increased over
the infinite case by the square root of the factor P/(P
- D). Given the fill rate, the optimum lot size
for that fill rate can be determined from the formula
above. Using the optimum fill rate, the optimum lot size
is determined. The results below assume the lot size
is unrestricted.
Compared to the model without shortages
and with an infinite replenishment rate, the optimum
lot size is larger by the ratio
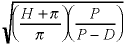 . .
The optimum inventory cost is reduced by
the inverse of the ratio.
|
|
| |
|
The
table shows the results for the optimum lot size and fill
rate
(q*=
1238, v*= 86.96%).
The instance results shown previously are
hidden in rows 15 through 26.
|
|
Fixed Charge in the Event of Shortage |
| |
The two remaining cases considered
on page involve backordered shortages with different cost models.
Here we consider a situation where the only charge associated
with a shortage is a fixed charge 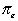 that
is incurred in any cycle that a shortage occurs. The charge
is independent of the number of customers that are affected. that
is incurred in any cycle that a shortage occurs. The charge
is independent of the number of customers that are affected.
The analysis for this case has the same
result as for the infinite replenishment case with
a fill rate of 0 and an infinite lot size. The production
rate is irrelevant since in the limit the demand is
not fulfilled until an infinite time has passed.
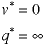
|
|
Fixed Charge for Each Unit of Shortage |
| |
Here we consider a situation where
there is a fixed charge 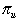 that
is incurred for each unit of shortage. The charge is independent
of the wait for the backordered item. that
is incurred for each unit of shortage. The charge is independent
of the wait for the backordered item.
The results are similar to the infinite
replenishment rate case except the breakpoint on the
fixed charge is reduced.

The optimum solution is the policy with
the smallest cost. Note that the first case suggests
an infinite lot size with all items backordered and the
second case suggests no shortages.
|
|
| |
|



