Here we consider the situation when the customer will not wait when the on-hand inventory is exhausted. Rather the customer will obtain the product elsewhere and the sale is lost. The replenishment to the inventory occurs at a finite rate.

Finite Replenishment Rate with Lost Sales

The inventory level is shown in the figure below for several cycles. The minimum level is 0. When the replenishment process begins inventory is added at the production rate P. Simultaneously, inventory is withdrawn at the demand rate D. When q units have been produced, production stops and the inventory level decreases at the constant demand rate until it reaches the 0 level. In the remainder of the cycle all demand results in lost sales.

Formulas for Instance Results

A single inventory cycle is shown below.

Since the demand is not entirely satisfied, the cycle time is a function of q and v. The times when production stops and when inventory is exhausted are given below.

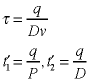
The table below shows the various revenue and cost components and their respective rates. The rates are the cycle costs or revenues divided by the cycle time.

Item	Amount during a cycle	Cost or revenue rate
Setup Cost	A
Product Cost	Cq
Holding Cost
Lost Sales Cost
Revenue from product Sales	Rq	RDv

For this model there are two decision variables q and v. We use the profit rate as a measure because the entire demand is not met and the profit is reduced when there are lost sales

Additional quantities associated with the inventory policy are below.

The measures are computed below for two examples using a lot size of 400 units and a fill rate of 90%. The figure shows a single cycle of the inventory pattern. The example assumes cost and revenue for the product are both zero. The lost sales cost includes both the lost profit and any additional charges associated with the lost sale. The case in column R has the lost sales cost of 1.2, while column S shows the case with a lower lost sales cost of 0.9. The results are not markedly different. We will see considerable difference in the results when the optimum solutions are presented.

Optimum Policy

For determination of the optimum lot size q* and fill rate v*, the unit revenue and unit purchase cost are included explicitly since a lost sale results in a lost profit. The objective is to maximize the profit rate. The profit is a concave function of the variables. Here we neglect the lower and upper bound on lot size.

The table below shows the parameters and instance results as well as the results for the optimum lot size and fill rate for two cases. The critical lost sales cost with this data is 1. The case in column R where the lost sale cost is 2 (>1) has the optimum values when there are no lost sales. For the case in column S with lost sale cost of 0.9 (<1) there is no inventory. It is cheaper to lose all sales than operate the inventory. We show q* as 0, but the lot size is irrelevant since no product passes through the inventory and all demand is lost.