|
|
 |
Stochastic
Programming |
 |
-
Simple Recourse Example: Product Mix |
 |
This example was borrowed from An Optimization Primer,
An Introduction to Linear, Nonlinear, Large Scale, Stochastic
Programming and Variational Analysis, by Roger J-B Wets,
January 11, 2005 (unpublished manuscript).
Consider a product mix problem. A furniture maker makes
four products: P1, P2, P3 and P4. Two manufacturing resources
are required: carpentry and finishing. The requirements
measured in hours per unit are known and shown in the table
below along with the profit per unit of product.
Product Parameters |
P1 |
P2 |
P3 |
P4 |
Carpentry Hours per
Unit |
4 |
9 |
7 |
10 |
Finishing Hours per
Unit |
3 |
1 |
3 |
4 |
Profit per Unit |
15 |
25 |
21 |
31 |
Our problem is to select the product mix to maximize total
profit, but the availability of the resources are not known.
Rather we have four equally likely estimates of the hours available
for each resource. The random variables that determine the
resource availabilities are independent.
Resource Distribution |
1 |
2 |
3 |
4 |
Carpentry Hours Available |
4800 |
5500 |
6050 |
6150 |
Finishing Hours Available |
3936 |
3984 |
4016 |
4064 |
Probability |
0.25 |
0.25 |
0.25 |
0.25 |
The mix chosen will require some number of hours for the resources.
This is called a decision making with recourse. We must chose
the mix before the uncertain quantities are known. Once the
uncertainty is realized we must make additional decisions,
called the recourse decisions, to adjust for the new conditions.
We use the notation below to describe the model with accuracy.
|
Expected Value Solution |
| |
The example problem is a product mix problem
with only four products and two resources. The problem has
four products with production amounts as x1 through x4.
The unit profits for the products are in the objective coefficient
row. The problem has two resources, carpentry and finishing.
The hours used for the products on the resources are shown
in the constraint matrix. The available hours for the resources
are uncertain. For the expected value solution we use the expected
resource availabilities as the RHS values.

The optimum mix includes P1 and P2. The solution uses all
available carpentry and finishing hours.

As illustrated previously, the expected value solution
is not very acceptable because there is a good chance that it
will not be feasible once the amount of resource availability
is revealed. In this case there is a 50% chance that there will
a shortage in carpentry hours and a 50% chance that there is
a shortage of finishing hours. Since the random variables are
independent, the probability that the solution is feasible is
only 25%.
Resources |
Used |
1 |
2 |
3 |
4 |
Carpentry Hours |
5625 |
4800 |
5500 |
6050 |
6150 |
Finishing Hours |
4000 |
3936 |
3984 |
4016 |
4064 |
Probability |
|
0.25 |
0.25 |
0.25 |
0.25 |
|
Recourse Costs |
| |
To model the problem with simple
resource, we prescribe costs for exceeding the resource
amounts available. These are the shortage costs. They might
represent the cost of paying workers overtime pay. We also
prescribe the costs for falling below the amounts available.
These are the overage costs. They might represent the cost
associated with idle workers.
For this example, the number of hours available for the
resources happens to be less than the amount used by the production
plan, there is a shortage of hours and extra hours must be
purchased to make up the shortage. The cost of extra carpentry
hours is $5 per hour and the cost of extra hours for finishing
is $10 per hour. There is no penalty for when the available
hours exceeds the amount used (overage). The costs are shown
in the table below.
Penalties |
|
|
Carpentry |
5 |
0 |
Finishing |
10 |
0 |
For the expected value solution, the penalties and their costs
are computed on the left below. The associated formulas are
on the right.
Although the profit of the expected value solution is 20761,
it must be reduced by the expected cost of hiring extra hours
for the resources. This reduces the expected profit
to 19373. The simple recourse model explicitly considers the
recourse costs, so a better solution should be available. |
Simple Recourse |
| |
To express the simple recourse
problem with a mathematical programming model, we rewrite the
constraints to explicitly determine the amounts of each resource
used and the objective to include the recourse costs. The objective
is written as a maximization to reflect the goal of the example
to maximize profit less the expected recourse costs.

For discrete distributions the expected recourse cost is a
piecewise linear function of 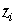 .
The calculation on the left shows the implementation of the
expressions on the right. The important information for the
math programming model are the piecewise costs and upper bounds
for each piece. .
The calculation on the left shows the implementation of the
expressions on the right. The important information for the
math programming model are the piecewise costs and upper bounds
for each piece.
It is an important result that the piecewise costs increase
as the index increases. Thus we have:

The expected cost is therefore a convex function of 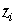 .
For example the expected cost for the carpentry resource is
shown below. Concavity assures that the result of the optimization
is a global optimum. .
For example the expected cost for the carpentry resource is
shown below. Concavity assures that the result of the optimization
is a global optimum.

The Math programming model for the simple recourse
problem is below. Two constraints represent the resource requirements
and two provide the piecewise linear expected recourse cost.
The optimum solution produces more P3
than the expected value solution. |
|
| |
The solution still has a 50% chance of using
all the carpentry hours available, but exactly 6050 hours are
used. This is one of the realizations of the discrete probability
distribution. The solution uses the smallest possible value
of the finishing hours available, so no extra hours are necessary.
Resources |
Used |
1 |
2 |
3 |
4 |
Carpentry Hours |
6050 |
4800 |
5500 |
6050 |
6150 |
Finishing Hours |
3936 |
3936 |
3984 |
4016 |
4064 |
Probability |
|
0.25 |
0.25 |
0.25 |
0.25 |
|
Side Model |
| |
This small problem is easily setup using the
model structure provided by the Math Programming add-in, but
the piecewise linear portion increases the extent of the A matrix.
The side model feature makes
a model that will be more efficient for larger problems with
more values for the discrete random variables. For the example
problem, we first constraint a linear programming model that
includes the variables z1 and z2, but not the
variables associated with the piecewise linear approximation.

We then choose the Side command from
the Math Programming menu and fill in the fields as below.
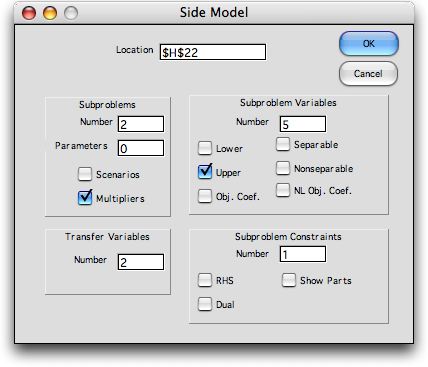
The side model form is constructed starting in
cell H22. The data for this problem has been filled in, but
the problem has not yet been solved. To
keep the model small we have taken advantage of the fact that
the probability values were the same for each random variable.
The multipliers in column I describe the costs of the extra
hours. The penalties are shown as negative values because we
are maximizing the objective function. The coefficients in the
range (N26:R26) show the coefficients of the piece-wise variables
and the coefficients in the range (S32:W33) show the upper
bounds on the individual pieces. |
|
| |
Solving the problem by clicking the Solve button
in the upper left corner of the LP model calls the Excel Solver.
The solution is shown below. The solution is provided in the
green areas of the worksheet. The solution is the same as for
the extended form of the LP. |
| |

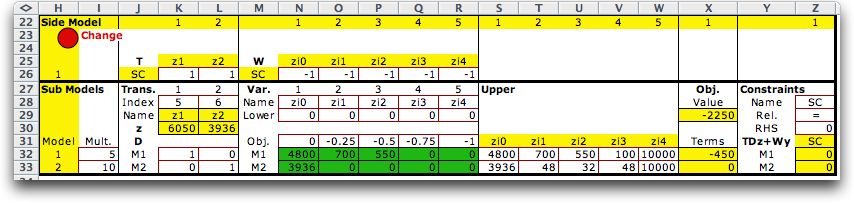
|
| |
Although not so obvious for this small problem,
the side
model feature makes
a model that is be more efficient for larger problems with
more values for the discrete random variables. The side model
grows linearly with the number of pieces in the discrete representation
and almost linearly with the number of random RHS values. |
| |
|
|



