For the multi-item system two or more items are stored and use one or more common resources. There are constraints on the limited resources. To construct a model, select the Optimize command from the menu and choose the appropriate option from the Optimization section of the dialog. Features of the individual inventories are selected with the buttons on the left. The objective function can be either to maximize total profit or minimize the total inventory cost. Default parameters for the inventory items are set with the Params button. The boxes on the right determine the constraints to be included in the analysis.

The Name is used by Excel to name several regions on the worksheet, so it must not include any spaces or punctuation marks. The Time Interval is the dimension for time related quantities. The Number Inv. is the number of items in the system.

Clicking OK, presents the nonlinear programming dialog from the Math-Programming add-in. This add-in must be installed or the model cannot be constructed. Although some settings of the dialog may be changed, it is best to simply accept the settings given by clicking the OK button.

The Math-Programming add-in constructs the nonlinear programming model and the Inventory add-in adds information for the inventory optimization. The complete worksheet for the example problem is shown below. The problem has already been solved. Each optimization model requires a separate worksheet.

The mathematical programming model is placed in the first 20 rows of the worksheet and the range for the inventory data is placed below, starting in row 23 for the example. The cells in rows 23 through 33, excluding rows 24 and 25, can be changed to reflect the data for the problem. The specific data included depends on the type of inventory defined by the dialog. In the example, we have chosen to have an infinite replenishment rate and allow no shortages. The data for the items has been selected for illustration.

Row 34 holds the lot sizes for the items. These cells have formulas that link their contents to the math-programming solution in row 8. The contents in these cells, as well as other yellow cells, should not be changed. They all hold Excel formulas.

Rows 35 through 39 hold functions provided by the add-in that compute quantities necessary for the constraints or objective function of the math-programming model. They all depend on the lot size in row 34.

The nonlinear programming model is repeated below for convenience.

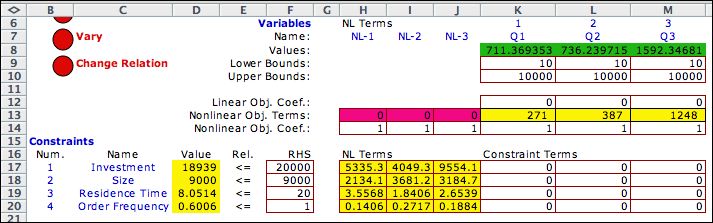
The variables for the model are the lot sizes of the three items. We use 10 as the lower bound and the default of 10000 for the upper bound. The lower bound is chosen to keep the lot size from going to zero, where some of the functions are undefined. The objective is to maximize net profit for the system. The linear coefficients are zero for this application. The nonlinear objective function terms all point to row 35 of the inventory definition where the profit for each item is computed.

We have selected four constraints for the example. The nonlinear terms for the inventory items appear in the yellow cells of columns H through I. The constraint values depend on the lot sizes and are computed in the Value column. The restrictions on the quantities are provided by the user and are listed in the RHS column. The model requires for each constraint that Value <= RHS.

• Investment: This constraint restricts the average inventory investment for the system. The yellow areas for this constraint hold formulas that multiply the item costs (row 29) by the mean values of the inventories (row 36). The sum appears as the quantity under the word Value. It is limited by the number in the RHS cell to 20,000. The constraint is loose for the optimum solution.
• Size: This constraint restricts the maximum space or size of the inventory. The yellow areas for this constraint hold formulas that multiply the item sizes (row 32) by the maximum values of the inventories (row 37). The total size appears as the quantity under the word Value. It is limited by the number in the RHS cell to 9,000. This constraint is tight.
• Residence Time: This constraint restricts the weighted residence times for the items. The yellow areas for this constraint hold formulas that multiply the weights (row 33) by the mean residence times (row 39). The sum appears as the quantity under the word Value. It is limited by the number in the RHS cell to 20 weeks. This constraint is loose.
• Order Frequency: This constraint limits the number of replenishment orders per time interval (per week for the example). The yellow areas for this constraint hold the inverses of the cycle times (row 38). The sum appears as quantity under the word Value.It is limited by the number in the RHS cell to 1 per week. This constraint is also loose.

Clicking on the Solve button automatically calls the Excel Solver, loads the model and initiates the solution procedure. Be sure to open and close the Solver dialog before using this button. If the model was created on a different computer, use the New Functions and Buttons command on the menu to create a new button.

Since this is a nonlinear programming model, the solution may not converge to a globally optimum solution. Try several different starting points for the variable values in row 8, and choose the solution with the greatest profit. There is no guarantee that the global optimum will be obtained by this process, but it improves the chance that a good solution will be found.

Shortages Allowed

When shortages are allowed the fill rates become variables in the model. The fill rate for an inventory is the proportion of the demand that is immediately satisfied from the inventory. The remainder of the demand is either backordered or the sale is lost. We illustrate the case when shortages are backordered.

The new variables are FR1, FR2 and FR3, the fill rates for the three items. We bound the variables from below by 0.1 so fill rates of zero are not allowed. By their nature, fill rates cannot exceed 1. The functions used for the constraints are the same as before except they will vary with fill rate as well as lot size.

With shortages, we can add a constraint on the average shortage cost. This is computed as the sum of the average backorder level and the backorder cost per week. The result is shortage cost per week. For the example we limit this to 30. The constraint is not binding for the solution obtained.

The inventory parameters are changed to include the backorder cost per week. The nonlinear terms in the Shortage Cost constraint are the backorder cost (row33) multiplied by the mean backorder level (row 40).