|
|
 |
Inventory
Analysis |
 |
Systems |
| |
|
Several WIP components combine
to form a system. Components are linked by the flow between
them and the add-in provides three general arrangements
by which they may be linked and two mechanisms by which
flow is engendered.
System models are defined by selecting the System
command from the Inventory menu. The top four
boxes on the system dialog hold the location, name, time
interval and the number of components in the model. We
use the rest of this page to describe the structure and
drive options. The models assume steady-state, deterministic
operation. Although some of the components use resources,
there is no scheduling of scarce resources. Although in
many ways the assumptions are not realistic, the models
should be useful in identifying the source and magnitude
of WIP accumulations and the resultant system cycle times. |
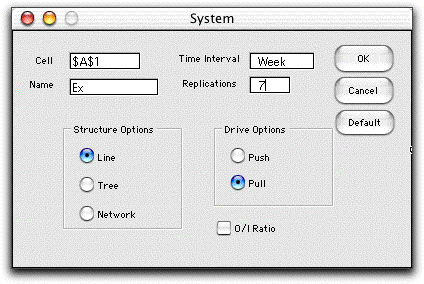
The structure and drive options are set with buttons on the
dialog. The structure determines the arrangement of the flow
paths in the system. For a line the flow passes through
the components in series. A tree either starts with
a single component and the flow diverges to multiple components,
or the flow starts with several components and converges to
a single output component. A network allows arbitrary
interconnections between components.
The drive option specifies the cause of flow through the process.
For the pull option, products are pulled from the outputs
of components. For the push option, items are pushed
into the inputs of the components.
The O/I Ratio button determines whether a component
will change the flow quantity as the flow passes from its input
to its output. In the examples linked to this page we will not
choose this option. For these examples, the flow that enters
a component will be the same as the flow that leaves. On the
Ratio page we illustrate cases where non-unity ratios
will be important to the models.
The seven different WIP components are shown in
figure below for a pull line. Since all components are placed
on the same data form, the row titles are not as explicit as
they are for only one component. The cells with x's indicate
the irrelevant parameters for some of the models. The setup
cost, setup time, processing time and maximum utilization are
not used for the delay, bank or lot size change components.
For every component the first variable row, row 12 for the example,
shows the input lot size and last variable row, row 14, shows
the output lot size. Between these two rows, row 13, the definition
of the variable depends on the type of component. For a delay
this cell holds the delay time. For the bank the cell holds
the bank amount. The cell is not used for the lot change component.
For all other components the cell is the processing lot size. |
|
|
|
We discuss
each of the drive/structure options below. Click on the link
on the section title to go to a page showing Excel worksheets
with numerical examples. In the following we use operation
to refer to a WIP component. |
| |
|
The line is a series of components that all carry the
same flow. The flow is either pushed from the first component
or pulled from the last. The two cases are illustrated
in Fig. 1. Click the link on the title at the left to
see numerical examples.
For the line system, the difference between push and pull
is a philosophical difference since for given parameters,
the results are the same for either case. The distinction
is important for the tree and network structures. We provide
the two cases for the line structure for completeness.
It is also easier to start the discussion with the line
structure because of its simplicity.
The term push is often used for systems driven by customers
who enter at the first operation to receive a series of
services. Push systems are sometimes analyzed by queuing
analysis because the interarrival time between sequential
customers may be a random variable. The service times are
also usually random variables.
The term pull is used to describe manufacturing systems.
A product must pass through a series of activities that
change raw materials into finished items. The system is
driven by the demand for the product. Sales draw finished
items from the last operation. Although manufacturing often
involves variability, the schedule of activities is sometimes
more controllable. The Just-in-time scheduling philosophy
implies that product is pulled by demand, rather than pushed
by raw materials entering the system.
Since our models neglect scheduling and variability for
the most part, the distinction between push and pull is
lost. Whatever is pushed into the first operation will
ultimately leave the last, and whatever is pulled from
the last operation must have previously entered the first. |
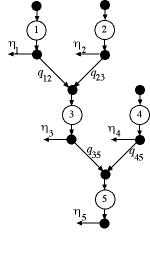
Figure 2
|
The generic pull tree is illustrated in Fig. 2. For this
structure the flow through each operation goes to a unique
following operation, while each operation may have several
input flows from other operations. This structure is
appropriate for modeling manufacturing processes where
raw materials are combined or mixed to produce a single
product. Product is withdrawn or pulled from the operation
with the greatest index, operation 5 for the example,
in an amount specified in the data. In addition to the
final operation of the process, our models also allow
flow to be pulled from the other operations. These flows
represent intermediate products. In general, we identify
the amount pulled from the output of operation i as  ,
the pull flow at operation i.
For the tree structures we require that the operations
be indexed so that when flow passes from operation i to
operation j, i < j. The greatest
index is m. For the example m is 5.
For the pull tree we identify the proportion,  ,
as the amount of the output of operation i required
for each unit of product passing through operation j.
The value of may
be any positive amount to represent a variety of manufacturing
situations. An assembly operation that requires one unit
of each input to be combined to produce one unit of a subassembly
would have the proportions equal to 1 for each input. A
mixing operation that combines inputs into a mixture would
have input proportions that sum to 1. An operation that
requires more than one unit of some input would be modeled
with a proportion greater than 1 on the associated input. |
|
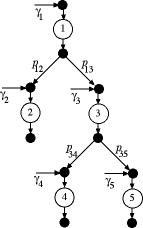
Figure 3 |
The generic push tree is illustrated in Fig. 3. For this
structure the flow into an operation comes from a unique
preceding operation, while the operation may have several
output flows going to other operations. This structure
is appropriate for modeling service systems where customers
arrive at a source node, node 1 in the example in the amount  .
In addition to node 1, flow may also be pushed into the
network at other operations. The flow entering at operation i is  .
Note that push flow enters the process just before an operation.
The flow that passes through an operation may be split
to go to other operations to receive different types of
processing. Units pass through the tree until finally they
are withdrawn to the nodes that have no successors, nodes
2, 4 and 5 in the figure.
For the tree structures we require that the operations
be numbered so that when flow passes from operation i to
operation j, i < j. The greatest
index is m. For the push tree we identify the
proportion,  as
the proportion of the output of operation i that
is passed to operation j. The value of may
be any nonnegative amount to represent a variety of situations.
For a splitting operation that separates the total flow
passing through operation i into several paths,
the sum of the proportions leaving i would equal
1. |
Pull
Network
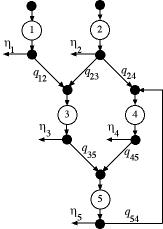
Figure 4 |
The pull network is illustrated in Fig. 4. For this structure
the flow through each operation may go to more than one
operation, and each operation may have several input flows
from other operations. This is a more general structure
than the pull tree structure. Flow is withdrawn or pulled
from any of the operations. Again we use as
the amount pulled from operation i. Indices are
assigned to the operations arbitrarily, however, it is
often convenient to assign the indices to be increasing
in the direction of primary product flow.
For the pull network we identify the proportion, ,
as the amount of the output of operation i required
for each unit of product passing through operation j.
The value of may
be any nonnegative amount to represent a variety of situations.
An assembly operation that requires one unit of each input
to be combined to produce one unit of a subassembly would
have the proportions equal to 1 for each input. A mixing
operation that combines inputs into a mixture would have
input proportions that sum to 1. An operation that requires
more than one unit of some input would be modeled with
a proportion greater than 1 on the associated input.
The example shows an arc passing from operation 5 back
to operation 4. In a practical instance, this might represent
the reworking of some part. Although we might be tempted
to identify  as
the proportion of the output of operation 5 returned to
operation 4, this is not correct for a pull network. is
the proportion of the flow through operation 4 that comes
from operation 5. Similarly,  is
the proportion of the flow through operation 4 that comes
from operation 2. |
Push
Network
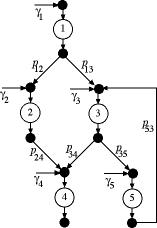
Figure 5 |
The push network is illustrated in Fig. 5. For this structure
the flow through each operation may go to more than one
operation, and each operation may have several input flows
from other operations. This is a more general structure
than the push tree. Flow is inserted or pushed into any
of the operations. We use as
the amount pushed into operation i. Indices are
assigned to the operations arbitrarily, however, it is
often convenient to assign the indices to be increasing
in the direction of primary product flow.
For the push network we identify the proportion, ,
as the amount of the output of operation i that
is passed to operation j for each unit of product
passing through operation i. The value of may
be any nonnegative amount. Typically for a service system,
the sum of the proportions leaving an operation is equal
to 1. This means that the flow is split among the several
following operations. It may be necessary to use other
combinations of proportions to represent different systems.
The example shows an arc passing from operation 5 back
to operation 3. In a practical instance, this might represent
the reworking of some part.  as
the proportion of the output of operation 5 returned to
operation 3. It is not necessary to define a proportion
for the flow leaving the system at operation 5. |
|
| |
|
|
