The Replication input allows strategies to be run more than once. When a randomized starting solution is used, it is best to run several replications of the strategy and choose the best of the local optima. The figures on the right shows the results of six repetitions of the strategy that begins with a random solution and continues through cycles of the insert, switch and turn statistics. Each repetition stops with a local optimum. The titles in column AI of the display are followed by one to three integer numbers. The first number is the repetition number, the second is the number of times the heuristic type has been visited during the strategy, and the third number is the cycle number within the visit.

Replication summaries are displayed on the Models worksheet as illustrated at the right. Columns identify the heuristic or initializing method, the number of runs, the number of runs finding improved solutions and the value of the best solution after the starting process or heuristic has been performed. (The time and run/second statistics are also shown on the worksheet, but not illustrated here.) Row 5 shows the initial solution and rows 6 through 14 show the first replication. The replication begins with a single random solution in row 6. The first two cycles of the Insert heuristic, in rows 7 and 8, result in 13 improved solutions, while the third shows no improvement. Two cycles of the Switch heuristic, in rows 10 and 11, yield 21 improvements, while the last in row 12 has none. The single turn cycle in row 13 shows no improvement. One more insert cycle is required to meet the requirement for a local minimum. When three heuristics are used, three consecutive 0's in the Improve column indicate a local optimum.

The objective value in row 14 is the objective value for a local optimum solution. Row 16 compares this solution to the value of the best solution obtained in the previous replications or the original solution.

Other replications repeat in like manner. Since all begin with different random initial solutions, each may terminate with a different local optimum. The Best Value column in rows 14, 24, 38, 48 and 59 are all different indicating that four local optimum solutions have been discovered. The best of these is in row 38.

The last replication is reported in a new column to avoid overwriting other contents on the worksheet. We see one more local optimum values in row 14.

The Total row reports 19419 runs with 191 improved solutions. The best solution has the value of about 245. The decision values and sequence values are reported on the model and result worksheets.

The buttons on column D of the Results worksheet initiate several built-in strategies. The Repeat field specifies the number of replications for the strategy. The first two buttons on the left are not affected by the number in this field, but multiple replications are useful for the last two strategies that involve random initial solutions.

The first button in column D evaluates the current solution without searching for a better solution. This might be useful when the analyst is adjusting a solution determined by the add-in. The current sequence is defined by the entries in column E of the Results worksheet. When the button is clicked, the sequence is transferred to the Model worksheet to evaluate the solution. Computed results on the Model worksheet are subsequently transferred back to the Results worksheet. The user-defined sequence must have no loops and must have a unique index in each row of column E.

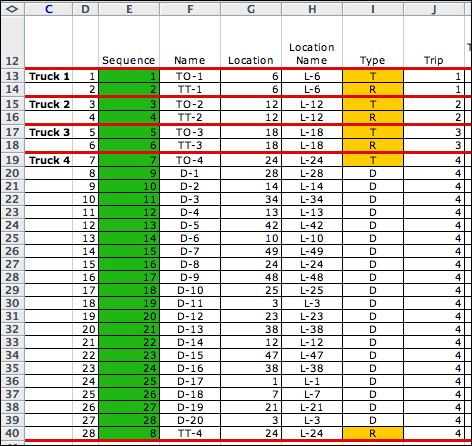
The buttons on the right side (column H) call VBA subroutines. The Initial Solution button creates a simple solution for the VRP problem illustrated at the right. The initial sequence is in column E. The example has four trucks and for the initial solution truck 1 through 3 have no deliveries, while truck 4 has them all. In general, when the plan has several trucks, the last truck handles all the deliveries. The route through the deliveries is determined by the delivery indices. This is usually not a good solution, but it provides a convenient starting point for illustrating the various options.

The Search button provides for a user-defined search as described below. The Map button creates a worksheet mapping the coordinates of the trucks and deliveries and displays the route in column E. The Google Earth button helps to create a Google Earth display of the results. This is described on a later page of this section.

The Improve Current Solution button on the left seeks a local optimum solution starting from the sequence in column E. The statistics on the right are for the simple initial solution pictured above. Only two insert cycles are used because the second insert cycle made no improvement. Three switch cycles, and a turn cycle completes the first replication. Since improvements occur after the insert cycles in rows 6 and 7, a second replication begins in row 12. The process is terminated when that cycle provides no improvement. It is interesting that this solution is better than the best found with six random starting solutions.

The Random Plus Improvement button generates a random solution and improves that solution to a local optimum. The random solution value is in row 6. The final solution is a local minimum.

The greedy initial solution is constructed in a manner that usually results in a better solution than a random start. As for the simple initial solution the first 3 trucks are assigned no deliveries and the last truck has all the deliveries. Rather than list the deliveries in order of index as for the simple initial solution, the greedy solution selects a random order for the deliveries. Then a cycle of the insert heuristic considers each delivery in order and places it in the position that most improves the objective value. Since this is a one-pass greedy process, it rarely obtains even a local optimum, but it leads to better initial solutions than a purely random start mechanism. In the example the result is reported in row 6.

The improvement strategy is then applied to obtain a local optimum. For the example, the final solution is even worse than the random start. There is no guarantee that a better initial solution leads to a better final solution.

Multiple replications are allowed for this option.