The Model worksheet is entirely constructed by the Routing add-in. Its purpose is to collect data from the Data worksheet, interact with the search algorithms in the Optimize Sequence add-in, and report solutions on the Results worksheet. Although users familiar with the add-ins may experiment by changing some features of this worksheet, in general it is better to leave it alone.

In the following we divide the model worksheet into three parts to simplify the discussion. The parts are different in function. The particular solution shown in the example is the same one illustrated on the Results page.

Optimize Model

At the top of the model worksheet shown below are the control buttons and the results of the most recent computation. Rows 10 through 19 hold the decision variables, the objective function, the current sequence and the distances between map locations. A similar form is constructed by the Optimize add-in as described on the Combinatorial Form page. The form is particularly adapted to the TSP on the Traveling Salesman page. Here we adapt the TSP form for the routing problem.

For this model we identify the items to be sequenced as nodes. Each node is related to a truck origin node, a truck terminal node or a delivery site. The nodes referring to trucks are indexed first. For example with two trucks, the first four nodes are TO-1, TT-1, TO-2, and TT-2. The last ten nodes relate to delivery sites, nodes 5, 6, ... 14 refer respectively to D-1, D-2, ... D-10. This one-to-one assignment does not change during the solution process. The relationships between nodes and the routing problem elements are stored on the Excel worksheet in rows 13 and 14.

We seek the sequence of nodes that gives the smallest value to the objective function in cell E12. E12 holds a formula that evaluates the complex cost model described on the remainder of this page.

There are some rules concerning acceptable sequences. The first rule is that the first node of the sequence represents the origin node of the first truck. For the example, node 1 representing TO-1 must begin the sequence. The second rule is that the last node of the sequence must represent the terminal node of the last truck. For the example, node 4, representing TT-2, must end the sequence. Further wherever a truck terminal node appears in the sequence, the origin node of the next truck must follow. We see this in the figure where the terminal node for truck 1 appears as the 7th node in the sequence. The origin node of truck 2 must be the 8th node of the sequence. This assures that every delivery is handled by exactly one truck. The enumeration process maintains these relationships.

Row 15 describes the sequence by indicating for each node the next node in the sequence. We see in E15 that node 13 (D-9) follows node 1 (TO-1). In Q15 we see that node 9 (D-5) follows node 13 (D-9). This process can be continued to find the complete sequence. The entries in row 15 are the variables of the problem. They are controlled by the program that implements the heuristic solution process.

Row 16 describes the sequence more directly by listing the nodes in sequence order. E16 holds the first node in the sequence, node 1 (TO-1). F16 holds the second node in the sequence, node 13 (D-9). G16 holds the third node in the sequence, node 9 (D-5). The process continues until the last node in the sequence is reached. This is node 4 representing the terminal node of the second truck, TT-2. Row 16 is computed with Excel formulas from decisions in row 15.

Row 18 holds the map distances between the locations of adjacent nodes in the sequence. For instance the value of E18 is the distance between the location of node 1 and the location of node 13. For the example, the location of node 1 is L-9, and the location of node 13 is L-6. E18 is the distance between L-9 and L-6. The numbers in row 18 are Excel lookup functions that reference a matrix further down on this models page.

For the example, the sequence is (1, 13, 9, 8, 6, 14, 2, 3, 11, 5, 7, 10, 12, 4). The colored indices in the sequence are nodes related to the trucks. The particular sequence defines the route (1, 13, 9, 8, 6, 14, 2) for truck 1. The route begins at the origin location of truck 1 and ends at the terminal location of truck 1. The route for truck 2 is (3, 11, 5, 7, 10, 12, 4). It begins at the origin location of truck 2 and ends at the terminal location of truck 2. The travel distances associated with the links of the trip are selected from the distance matrix using a LOOKUP equation. For example, the value, 8.83899, in cell E18 is the Euclidean, or straight-line distance, from node 1 to node 13. The other entries in row 18 are similarly computed.

Data Cells

Results Cells

The results cells starting in row 41 are controlled by the current sequence. All the cells are colored yellow to indicate that they contain Excel formulas. The columns are ordered by the current sequence. The display is dynamic in that the columns change as the decision variables in row 16 change. For each trial solution, the objective value is computed from this portion of the worksheet.

The sequence of trucks and delivery nodes is in row 42. Row 43 identifies the type of the node, T for origin truck nodes, R for truck terminal nodes, and D for delivery destinations. The trip row (44) gives an integer index that indicates the components of the sequence that are assigned to the various trips. The current example has two trips representing the routes of the two trucks. The times available, early times, site times, late times, and local travel times are transferred by index functions from the data cells. An arrival time in row 47 is computed as the sum of departure time of the previous node plus the travel time to the next node. If this turns out to be earlier than the time available, the time available becomes the arrival time. The departure time in row 50 is computed as the arrival time plus the site time. The travel time to the next node in row 52 is the sum of: the local travel time from the current node to its map location, the map travel time between the current node and the next node, and the local time to the next node.

Row 46 shows the arrival time at each node and row 50 shows the corresponding departure time. Notice that starting at truck 1, the times increase through the route of truck 1 until the terminal node for truck 1 is encountered. The terminal node for truck 1 is immediately followed by the origin node for truck 2. The arrival time for truck 2 is 480. This is the beginning of the second trip. The second trip occurs simultaneously with the first trip. The second trip is completed by the terminal node for truck 2.

The evaluation of the sequence in terms of the early and late times and the resource shortages begins on row 54. Row 55 shows the deliveries that are early, D-4 and D-6. Row 56 shows the deliveries that are late, D-1 and D-3. Row 57 shows the cumulative capacity for the sequence. When a new truck is assigned to a trip, the cumulative capacity for the trip is the capacity of that truck. As the truck visits delivery nodes, the loads of the delivery sites decrease the cumulative capacity. A negative number in this row indicates a shortage. Row 58 reports the amounts of the shortages. Since the current sequence has no shortage, the contents of this row are 0.

Rows 61 through 65 numerically evaluate the solution. Row 61 shows the travel costs. The duration costs in row 62 are computed by multiplying the departure times by the duration penalties. The example uses 0 as the duration penalties, so the entries are all 0. The early and late costs multiply the sum of the early and late amounts by the penalties for these factors. The contributions of each node to the objective function are computed in row 66. All the costs and penalties are accumulated in column T that is not shown in the figure. The total amount is transferred to the objective function cell E12 at the top of the worksheet.

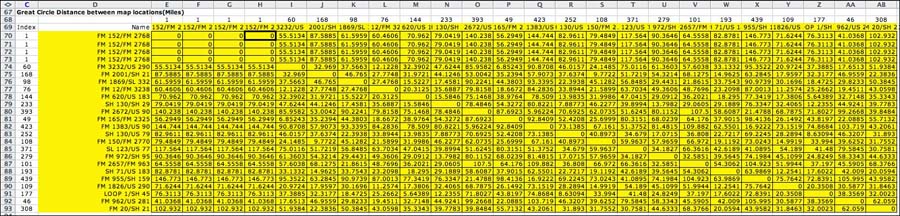
Distance Matrix

Starting in row 67 is a square matrix holding the distances between the map locations in the plan. This matrix addresses data on the distance worksheet. When a table provides intersite distances and the distance page, the entries to the matrix on the model page are simple lookup functions addressing the distance matrix. When the locations are described by the Cartesian coordinates, the entries in the model matrix are equations computing the Euclidean matrix (Pythagorean theorem). When the locations are described by the geometric coordinates, the entries in the model matrix are equations computing the Great Circle distance.

In all cases the matrix does not change with the solution, so the computation time associated with building the matrix is experienced only when the matrix is created by the add-in. This speeds up computation during the solution process.

Location Coordinates

Sequence Optimization

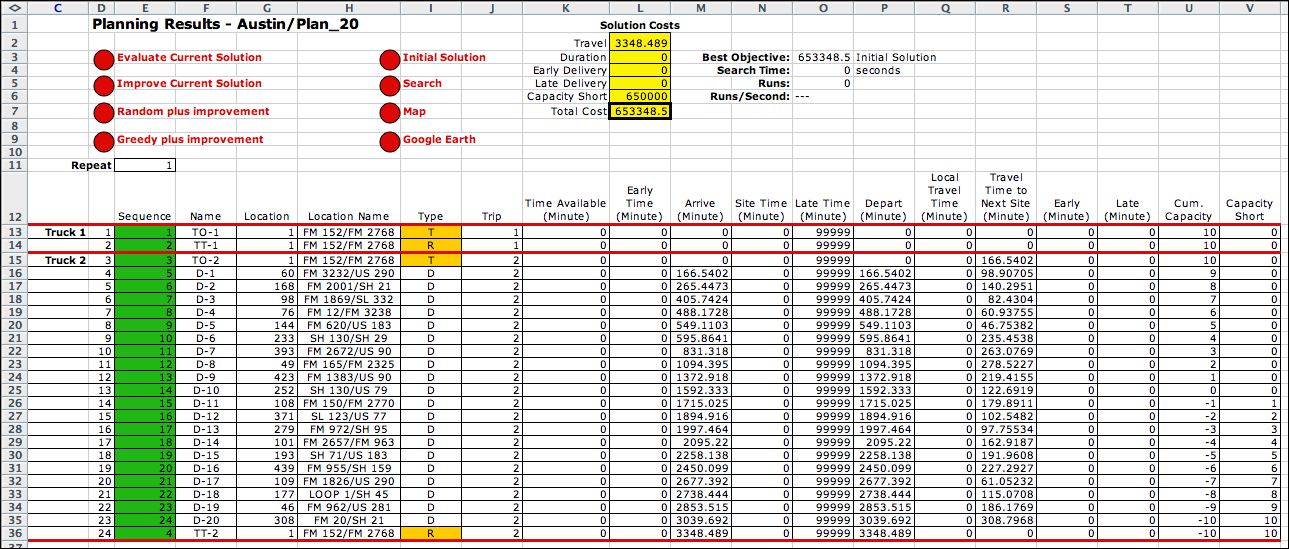
The Optimize Sequence add-in is used to search for the optimum sequence. To illustrate the solution process, we will use the initial solution shown below. The initial solution is created by clicking the Initial Solution button on the Results worksheet. The solution is feasible, but it assigns all the deliveries to the last truck. We will use search heuristics to find a better solution.

Because it uses heuristic procedures there is no guarantee that the search will obtain the optimum solution unless all possible sequences are examined. The algorithm incorporates several search heuristics that are designed for general sequence problems but adapted for the routing problem. The process manipulates the variables in the green cells of row 15 and observes the resultant objective function in cell E12.

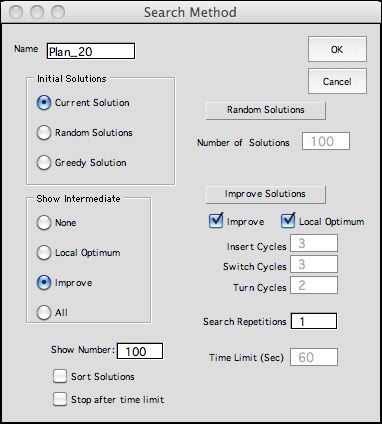
To improve the current solution, click the Search button at the top of the worksheet. The dialog below is presented. Click the Improve checkbox at the right side of the dialog. Also check the local optimum box. The Improve button on the left of the dialog indicates that you want to review all the improved solutions encountered by the process.

Although an acceptable solution was obtained for this small problem, the search becomes more difficult as the problem size grows. It also becomes more difficult as we add complexity to the problem by making the early and late times restrictive and as more resources are added. The worksheet evaluation for each solution depends on the size of the problem. Even one pass through the improvement process takes a large number of individual evaluations.

Buttons

At the top of the page there are four buttons. The first button displays the Search dialog shown earlier. The Map button creates the map of the current solution. This is the same map as the one created by a similar button on the results page. The buttons on the right open the unique Results worksheets corresponding to the Model worksheet. The yellow cells in the Model worksheet are linked by formula to the data on the Data worksheet. Any value changes there are immediately reflect on the model worksheet. If the number of trucks or deliveries is changed the model worksheet must be regenerated by the button on the data worksheet.

To the right of the buttons are statistics concerning the computations obtaining the solution. The example required 4083 solution evaluations (called runs). The average number of runs per second depends on the speed of the computer. The runs per second decreases as the size of the problem increases. The total search time is 44 seconds. A local optimum was obtained.

The heuristics used for searching the solution space are described on the next page.