The Traveling Salesman Problem is to find a sequence of cities such that the length of the distance traveled on the tour through the cities is minimized. An example 10 city problem is shown below. The form shows 11 cities since the first and the last repeats city 1. The distance matrix is randomly generated and represents the intercity distances when the cities are placed randomly on a plane. Row 7 shows the decision at each city that gives the next city to be visited. Row 8 shows the corresponding sequence. This initial solution visits the cities in numerical order. The tour length for this solution is computed in cell D3 and is 301. The contents of cells F2 and F3 are not relevant for this problem.

The add-in includes improvement algorithms specifically adapted for the TSP. To improve this initial solution we choose Search from the menu, click the Current Solution button and click the Improve checkbox. We enter 2 in the n_change field. The Change field is not used for the TSP. We explain the Assume Linear Objective box later.

The 2-change heuristic operates on the sequence. City 1 is fixed. Each pair of cities, not involving 1 or 11, is considered in turn and the elements of the sequence vector for these two cities are switched. For the example, the first three sequences considered are shown in the table.

Considering the nine cities that may be switched, there are 36 possible switches. For each case, the decisions leading to the sequence are placed in the decision vector on the worksheet and the worksheet formulas compute the tour length. If an improving switch is observed the sequence is changed and the remainder of the switch operations are performed on the new sequence. The 2-change procedure is repeated until a pass through the possible switches is completed with no improvement.

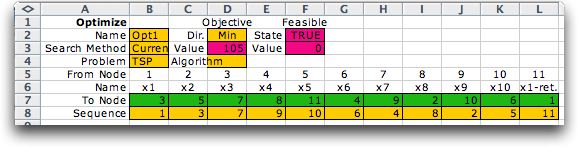
The table below shows the result of the 2-change procedure for the example. Row 3 shows the run statistics. The best solution observed has a tour length of 105. Each pass requires 37 runs (1 to evaluate the starting solution and 36 to evaluate each pairwise switch). The example required five passes through the 2-change procedure totaling 185 runs. The 2 runs indicated in the cell labeled Enum. counts the first and last solutions. The program estimates the number of runs required for the improvement assuming that three passes will be necessary. The estimate may be in error because the process will finish in a single pass if there are no improvements to be made or the process may take several passes if there are a number of improving switches.

The individual lines of the table show the decisions defining the tour, not the tour itself. The optimum tour starts at city 1 and travels to city 3. From city 3 the tour goes to city 7. The complete tour is shown as the sequence in row 8.

The dialog also allows the improvement process to start from a greedy solution of the TSP. The greedy solution has a length of 107. The improvement process finds a tour of 105 with the sequence shown below. It is a different tour than the one above.

The 3-change procedure selects 3 elements in the sequence and evaluates all permutations of the three elements. The program evaluates only permutations that are different from the incumbent solution in all three elements. This reduces the number of duplicate sequences evaluated. When the dialog specifies the 3-change procedure, the add-in first performs the 2-change procedure until no improvement is observed and then performs the 3-change procedure. The 3-change heuristic applied to the tour just above found no improvement.

The user can specify larger values for n_change, but the number of runs will certainly grow.

Improving Random Solutions

Improvements may also be applied to randomly generated sequences. In the dialog below, we specify that 10 random sequences are to be generated. Each sequence will be improved with the 3-opt procedure.

Although we have illustrated the improvement algorithms using the TSP, they are appropriate for any sequencing problem that can be evaluated using Excel functions. The add-in provides the search algorithms, but worksheet formulas evaluate the solutions.