|
|
 |
Optimize |
 |
-
Fibonacci Enumeration |
| Single Variable |
| |
To illustrate the Fibonacci enumeration
and compare it with exhaustive enumeration we use a forecasting
example as in the figure below. The example was constructed
with the Forecasting
add-in. It uses a simulated time series with random step increases
and decreases in the mean value. This example is simulated for
200 periods beyond a 20 period warm-up interval. The forecast
of interest is 2 periods beyond the current period. For example
the forecast at time 2 is based on the estimate of the time
series mean at time 0. Note that if you are running the example
from the demo worksheet the Forecasting add-in must
be installed. To assure that the formulas on the worksheet are
linked to the add-in, choose the Relink command from
the Forecast menu.
The exponential smoothing method requires a single continuous
parameter alpha that ranges from 0 to 1. To convert
the search for an optimum alpha to a discrete space
we use a transformation common in forecasting practice:
alpha = 2/(m + 1) where m
takes on integer values.
The value of alpha used for the figure below is computed with
m = 11, the value that turns out to be optimum. We
use the Mean Average Deviation (MAD) computed in cell
S8 as the criterion for optimality. We are to find the value
of m that minimizes the MAD. In practice such a result
is useful because it suggests the best parameter for forecasting
a particular time series. |
| |
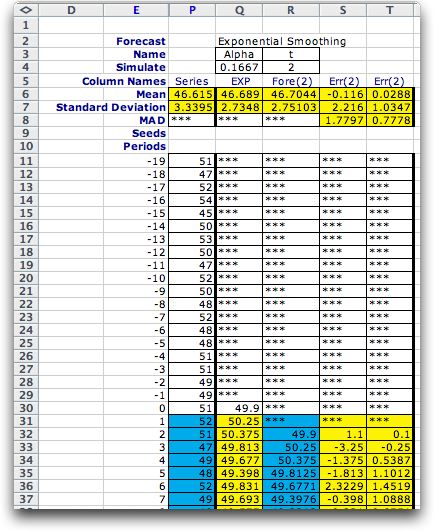
The example continues to 200 periods.
|
| |
The example has a single decision variable that ranges from
1 to 20. To create the form we choose the Add Form option
from the menu and set the parameters as below.
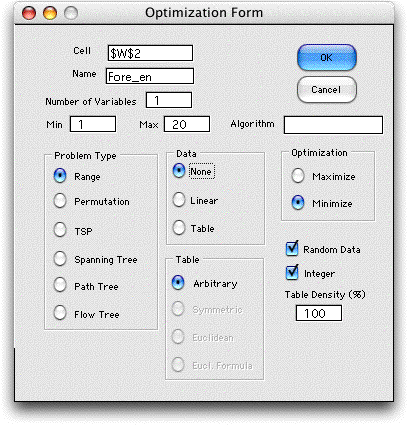
After the form is constructed we choose the Fibonacci search
method.
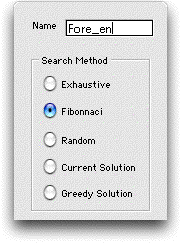
Fibonacci
search is based on the Fibonacci sequence. The first two Fibonacci
numbers in the sequence are both 1. All others are obtained
by adding the previous two numbers in the sequence. The first
ten Fibonacci numbers are shown below.
N |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
Fib. No. |
1 |
1 |
2 |
3 |
5 |
8 |
13 |
21 |
34 |
55 |
This search method is valid if the objective function
is unimodal. For a minimization this means that is it has no
more than one change in direction as the variable is increased.
We will see that for this example the MAD when m =1
is 2.2367. As m increases the MAD decreases until its
value is 1.7797 at m = 11. Thereafter the MAD increases
as m increases. Thus the MAD is unimodal in this case.
With N observations, this search method can find
the optimum integer value in an interval of length F(N + 1),
where F(N) is the Nth number in the Fibonacci sequence.
For the example we are searching the integers
1 through 20. We take the initial interval as 0 to 21 since
the search procedure does not enumerate the end points. We note
that F(7) = 21, so 6 observations are necessary. The results
are shown in the table below. The observations are placed according
to the numbers in the sequence. To search the interval of 21,
the first two observations are at 8 and 13. The value at 13
is the smaller, so the optimum cannot lie below 8. The interval
is now (8, 21) and the two observations are at 13 and 16. Since
the objective at 13 is already known, only the value at 16 must
be computed. Since the value at 16 is greater than at 13, the
interval that holds the optimum must be (8, 16). To further
reduce the interval, an observation is placed at 11. Since this
value is smaller than the value at 13, the interval is now (8,
13). The next observation is at 10. Since the objective at 10
is greater than at 11, the interval is now (10, 13). The last
observation is at 12. Again this value is greater than at 11,
so the interval is reduced to (10, 12). Only the observation
at 11 is within this interval and the optimum has been discovered.
At termination, the optimum value (11) is repeated and appears
in the list as run 7. |
|
| |
The search process requires that
the cell holding the value of alpha, Q4, be linked
to the decision variable at X8. This is implemented for the
example by placing the following formula in Q4.
= 2/(X8 + 1)
Note that the formula linking the combinatorial
variable to the model variable need not be a simple assignment
(=X8), but can be an arbitrary function of the combinatorial
variable.
Similarly, the objective for the problem must
be placed in cell Z4. We do this by placing the following formula
in cell Z4.
= S8
Cell S8 holds the value of the MAD for the simulated
time series. The process sequentially places the six values
of the decision variable in cell X8 and the value of the MAD
is computed for each decision alternative with the formulas
on the worksheet. The code of the add-in controls the search
process.
We do not use the feasibility cells, AB3 and AB4,
since there are no logical conditions that restrict feasibility
other than the limits on the variable. It is important that
the default value TRUE remain in cell AB3 since all solutions
generated are feasible.
For comparison, we show the exhaustive enumeration
below. Exhaustive enumeration requires 20 observations. The
feature of unimodality can be seen from the unsorted list of
results in column AR. Since the function is unimodal, both methods
find the optimum solution. Run 21 recomputes the optimal solution. |
|
| |
We must observe that the MAD for
a finite forecast is not always a unimodal function of the parameter
m. It is often the case that for simulated data the
objective will be "bumpy". The expected value of the
MAD may be a unimodal function of the parameter, but the average
of a simulated realization may not. In these cases the Fibonacci
method must be viewed as a heuristic. We use it to
reduce the number of observations required to obtain a solution,
but accept the fact that the method will not always yield the
optimum solution. |
More than one Decision Variable |
| |
We also allow the Fibonacci method
to be used with more than one decision variable. We use as an
example the same time series as before, but now we forecast
with the exponential smoothing
with trend method. This method estimates a constant term
and a linear trend coefficient. Forecasts are made with a linear
projection. In the figure below the constant term is in the
column labeled Exp. a, and the linear coefficient is
in the column labeled Exp. b. The forecast interval
is 2 and the forecasted values are in the column labeled Fore(2).
To illustrate, we compute the forecast in period 2 from the
constant and linear terms shown for period 0 (row 30).
F(2) = a(0) + 2*b(0)
= 49.7143 + 2*(-0.0195) = 49.6742
The error shown in Err(2) is the difference
between the observed value at period 2, 51, and the forecast.
The values of a(t) and b(t)
depend on the data of the previous periods based on the forecasting
method. This method has two parameters alpha and beta.
We would like to choose these two parameters to minimize the
MAD, the mean absolute forecast error, computed in cell T8.
The values shown in cells Q4 and R4 are the best values determined
by the enumeration. |
| |
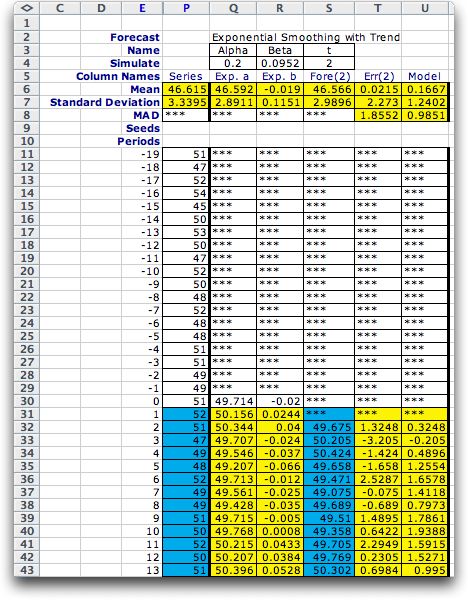
The example continues for 200 periods
|
| |
To find the optimum parameters,
we construct the form below using the Add Form menu
command with two decision variables. The forecasting parameters
in Q4 and R4 are linked to the variables in Y8 and Z8 with the
formulas:
alpha = 2/(Y8 + 1), beta =
2/(Z8 + 1)
The objective value in AA4 is linked to the MAD
with the formula:
value = T8
With more than one decision variable, the Fibonacci
method finds the optimum solution sequentially. With the range
1 to 20, each Fibonacci search requires six observations. The
variables are considered from left to right. For each value
considered for x1, six observations are made to obtain the optimum
value for x2 and the associated optimum objective value. Since
there are 6 values for x1, a total of 6*6 or 36 observations
are required to find the best solution.
The results are shown below. We also show the
best 20 solutions found during the search. It is not surprising
that the value for x2 (m for beta) is large.
The simulated time series only has step changes, not trends,
so the best value of beta should be as small as possible
(x2 should be as large as possible). |
|
| |
For comparison we show the solution
obtained by exhaustive enumeration. Exhaustive enumeration requires
20*20 or 400 observations. As expected the time required to
obtain the optimum is greater. For the example, exhaustive enumeration
yields the same solution as Fibonacci search. We see new solutions
among the top 20 solutions because exhaustive enumeration evaluates
so many more solutions than the Fibonacci method. |
|
| |
Discrete Fibonacci search only
works reliably when there is a single decision variable and
the objective function is unimodal with respect to that decision
variable. In a multivariable problem, there is no guarantee
that an optimum solution will be found. We provide this option
because many fewer solutions need be evaluated than for exhaustive
enumeration when the range for the decision variables is large.
For many problems the results will be nearly optimal.
As for exhaustive enumeration, Fibonacci search requires an
exponentially increasing number of observations as the number
of variables is increased. When only two values for each decision
variable are feasible (say 0 and 1), the two methods require
the same number of observations. Only when the range is greater
than 3 will the Fibonacci method result in a reduction. When
the range is large, the reduction in the number of observations
is considerable. |
Feasibility |
| |
In this example there were no
additional conditions limiting feasibility. Thus cells AC3
and AC4 play no role for the example. In other situations,
the State
cell (AC3) may contain a Boolean expression indicating by the
state TRUE or FALSE whether the solution is feasible or not.
For the Fibonacci method we must also provide a measure of
infeasibility in the Value cell. This is a formula
that returns positive values for infeasible solutions. Although
a 0 value for a feasible solution is desirable, the program
neglects the value for feasible solutions.
For infeasible solutions a term is added to the
objective value that is:
infeasibility measure squared multiplied
by the infeasibility weight.
The infeasibility weight is entered in
the Search dialog. Its default value is 10. Since the
algorithm treats all problems as minimizations, solutions far
from feasibility will be penalized with very large objective
values. This forces the Fibonacci search to select solutions
that are feasible rather than infeasible. Also if the method
compares two solutions that are both infeasible, the procedure
will judge the one with the least infeasibility as the better
one. |
| |
|
|



