Consider a directed graph consisting of n nodes. There is an arc between every pair of nodes, so the graph is said to be complete. A directed spanning tree consists of n-1 arcs selected so that the arcs define a unique directed path from a designated root node to every other node. The figure below shows a tree with 7 nodes where node 1 is the root node.

This and the next two pages describe three combinatorial tree problems: spanning tree, path tree and flow tree. In each case we are seeking a directed tree that maximizes or minimizes some measure. Although some instances of these problems are among the simplest of combinatorial problems, we address them all using enumeration and search approaches. With the Optimize add-in all the computations are very general. The Combinatorics add-in provides a less general but more efficient treatment of the spanning tree.

For convenience we will always use node 1 as the root node. Notice that every tree arc points to a unique node. Thus the arc from 2 to 4 points to 4 where no others point to node 4. We represent a tree by defining for node i the variable xi, where xi is the index of the node that begins the tree arc that terminates at node i. For example x4 = 2 implies that arc (2, 4) is part of the tree. The unique representation of the example tree is provided by the combinatorial variables shown.

Spanning Tree Problems

For the minimal or maximal spanning tree problems, each arc is assigned a length. The goal of the problem is to select a spanning tree so that the total of the lengths of the selected arcs is minimized or maximized. We illustrate the problem with the maximal spanning tree problem. To create the problem we choose Add Form from the menu and click the appropriate button.

The initial tree connects all the nodes directly to node 1.

The add-in places the combinatorial form on the worksheet with the upper-left corner located at the cell specified in the dialog. The lengths for a 7 node problem are shown below in the range labeled C(From, To). The table holds randomly generated symmetric data. Row 0 is used by the program and should not be changed. The variables defining the tree are placed in row 7 and the contributions of the tree arcs are computed in row 9 using the Excel Index function. The objective in cell D3 is the sum of the values in row 9. The Feasibility state and value in cells F2 and F3 are not used for the example.

Selecting Exhaustive Enumeration from the search example displays the following estimate of the number of trees for this network.

We know of no exact way to count the number of directed spanning trees for a complete graph and the number given is an overestimate. The example with 7 nodes has 16807 unique trees. The results showing the best 19 trees are below. The enumeration process only evaluates valid spanning trees.

The optimum tree and associated combinatorial form are shown below.

Although we have solved the problem by enumeration, there is a much simpler way to find an answer for this symmetric problem. We will show that in the next section. There are other spanning problems that are not as simple. For instance a directed spanning problem with an asymmetric length matrix does not have a simple algorithm. We might also add feasibility conditions such as there can be no more than two tree arcs leaving any node. The optimum for the example violates that condition for node 1. There is no easy way to solve this problem.

It is possible to formulate spanning problems as integer programs, but the models are not intuitive. An obvious formulation has 0-1 variables for each arc and constraints that require that an arc enter each node. Without cycle elimination constraints, however, the solution to this model may have cycles. There are constraints that eliminate cycles, but the number of such constraints grows exponentially with the number of nodes. The combinatorial approach is not hampered by cycles, because no arc is added to a partial tree if it forms a cycle. Only valid spanning trees are enumerated and evaluated.

Greedy Solution and Heuristics

The spanning problem with symmetric lengths can be readily optimized by a greedy algorithm. One method is called Prim's Algorithm described elsewhere on this site. For the minimal spanning tree, the greedy approach constructs a solution by starting from the root node and adding the arc with the smallest length to obtain a tree with two nodes. The algorithm then proceeds by finding the arc with the smallest length that extends the current tree to one additional node. The process continues until n-1 arcs are selected and all nodes are connected. The maximal spanning tree is constructed in a similar fashion, but the arc with the greatest length is added at each step.

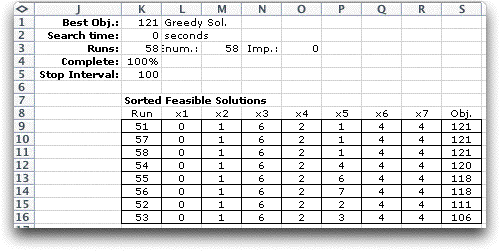
The add-in implements this method when Greedy is selected from the Search dialog. The results for the example are below. There is no point using using an improvement step, since the greedy approach finds the optimal solution. There are 58 evaluations required for the greedy approach. To find the node to add to the tree in each step, the program evaluates every possible addition. Although Prim's algorithm can be performed with many fewer computations we use the method of evaluating the worksheet as the principal tool for making decisions. This makes the greedy approach used here applicable to the other tree problems that may not be so simple. The results below show the feasible solutions generated by the greedy approach. The solutions that do not form a complete tree are not feasible and are not shown.

For the asymmetric case and for all other spanning tree problems the search dialog allows random searches and improvements.

For tree problems we only allow one kind of improvement. Given a tree, we investigate each nontree arc, say arc (i, j) . We form a new graph by adding this arc and deleting the arc formerly entering node j. If the new arc does not form a cycle, we evaluate the resultant tree. If the objective is improved, we make the revised tree the incumbent solution and continue the process. The improvement step is continued until a complete pass through the nontree arcs results in no improvement.

It is not necessary to include a data table with the combinatorial form. Without the form the user must compute the evaluation measure on the worksheet and put a link to the measure in objective value cell of the form. The add-in generates tree solutions and selects the optimum.