An example is shown below with
symmetric random data. One additional parameter is required
for this model and is placed in cell F4. This is an exponent
(Exp.) that will be used in the objective function. For a minimization
problem the exponent will be between 0 and 1, inclusive.
Several new rows appear in the form for a flow tree, row 8
holds the node flows and row 9 holds the arc flows. The node
flows are data items which for simplicity we make all 1's for
the example. In general the node flows should be nonnegative
numbers.
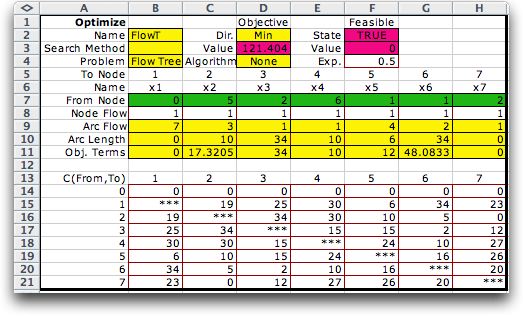
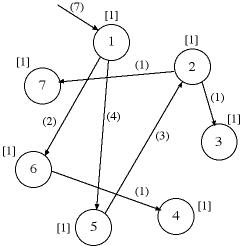
To explain the problem we use the solution shown in row 7.
Recall that the value of a variable tells the node that originates
the arc that enters a particular node. For example x2=5 implies
that arc (5, 2) is part of the tree. The initial tree is illustrated
in the figure below. The node flows are shown in square brackets
on the figure and the arc flows are in parentheses. The node
flows may be viewed as demands for some material at the nodes.
The tree arcs are to deliver the demanded quantities and the
materials enter the network at the root node (node 1). The flow
in the tree arcs are determined by conservation of flow. For
example, since the arc (2, 3) serves only node 3, the flow on
this arc is 1. Arc (5, 2) serves nodes 2, 3 and 7, so it must
carry 3 units of flow.
Given the tree designation in row 7 on the worksheet,
the arc flows are computed in row 9 by Excel formulas. Row 10
holds the unit costs for the arcs selected for the tree. Row
11 computes the product of the unit cost multiplied by the arc
flow raised to the power of the exponent. Rows 9 through 11
are colored yellow to remind the user not to change these cells.
The objective function for this problem raises
the flow to the power of the exponent given in cell F4 and multiplies
the result by the coefficient in the objective coefficient table.
Since the example uses the exponent 0.5, this is equivalent
to multiplying the coefficient by the square root of the flow.
This value is computed for each arc in row 11. The sum of the
values in row 11 is in cell D3 and is the objective to be minimized.
The minimal spanning tree problem and the shortest
path problem are special cases of the flow tree problem. With
the exponent at 0, an arc with nonzero flow contributes exactly
the arc coefficient to the objective since any positive flow
raised to the 0 power is 1. Thus, solving the problem with a
0 exponent will obtain the minimal spanning tree. With the exponent
1, an arc with nonzero flow adds to the objective the arc coefficient
multiplied by the flow. This is the same contribution that an
arc adds to the objective for the shortest path tree. Thus,
solving the problem with the exponent 1 obtains the shortest
path tree. We illustrate these two solutions later.
When the exponent is strictly between 0 and 1,
the objective is a concave function of flow, assuming positive
coefficients. This kind of problem is difficult because the
associated math programming model has multiple local minima.
For the math programming model, every tree is a basic solution
and every basic solution may be a local minimum. Thus the flow
problem for exponents strictly between 0 and 1 is difficult
and must be solved by combinatorial methods.
We use exhaustive enumeration for the example
problem with the best 20 solutions shown in the table below. |



