As for the spanning tree problems, we assign a length to each arc of a directed complete graph. For the path problem, the goal is to select a spanning tree so that the length of the path to each node is minimized or maximized. For an example, the length of an arc might represent the travel time for a vehicle. Emergency vehicles are located at the root node and we wish to find a travel path from the root node to a specified destination that has the smallest total travel time. In fact we want to find set of paths from the root node to all other nodes such that the length of each path is minimized for its destination. It is not hard to show that there will be an optimum solution such that the arcs in the collection will form a spanning tree.

With the Optimize add-in all the computations are very general. The Combinatorics add-in provides a less general but more efficient treatment of the path tree.

To illustrate we construct a combinatorial form for a network with 7 nodes.

The optimum solution is pictured below.

The form showing the optimum is below.

Greedy Solution and Heuristics

The problem with nonnegative and symmetric arc lengths can be solved by Dijksta's algorithm described elsewhere on this site. This is a greedy approach that constructs a solution by starting from the root node and adding the arc with the smallest length to obtain a tree with two nodes. The algorithm then procedes by extending the tree to an additional node such that the length of the path to the node passing only through nodes already in the tree is minimized. The process continues until n-1 arcs are selected and all nodes are connected. When the arc lengths are nonnegative and not symmetric, this method yields a tree that is not necessarily optimum. Although not symmetric, the greedy algorithm does reach the optimum for the example.

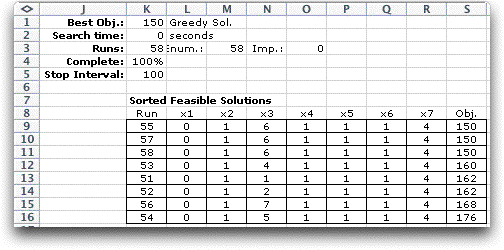
We illustrate the improvement process by starting from the solution given at the top of this page (the nodes visted in numerical order). The results are below. The initial solution is at the bottom of the list and subsequent improved solutions appear above it. The improvement approach is the same as for the spanning tree. Each nontree arc is inserted in the tree and the current solution arc terminating at the same node as the entering arc is deleted. If a cycle is not formed, the solution is evaluated. An improved solution replaces the current incumbent.

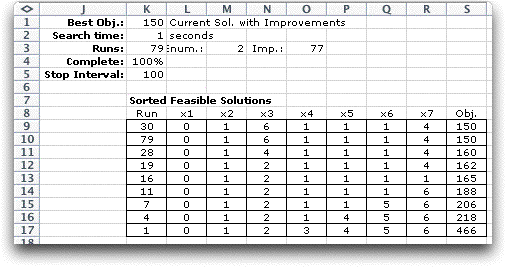
The improvement process we have described is equivalent to the steps that would be taken by the primal simplex method using a similar rule for selecting the variable to enter the basis. The improvement process will in fact always yield the optimum for the linear path problem, so it is never necessary to perform exhaustive enumeration or make random searches.

For the linear path problem with nonnegative costs, the greedy approach yields the optimum for symmetric problems and the improvement approach applied to an arbitrary initial tree yields the optimum for asymmetric problems. A time consumming combinatorial approach is only necessary if the problem is complicated in some way by adding constraints on feasibility or making the problem nonlinear. The latter is illustrated on the next page.